
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABC có A=90 độ=>tam giác ABC vuông ở A
áp dụng Py-ta-go :
BC2=AB2+AC2
=>102=AB2+(căn 75)2
=>100=AB2+75
=>AB2=25=>AB=5(cm)
câu b tự lm nhé bn,dễ lắm
Xét tam giác ABC có A=90 độ
=>tam giác ABC vuông ở A ( theo định lí Pytago đảo)
Theo định lí Py-ta-go ta có:
BC2=AB2+AC2
=>102=AB2+(\(\sqrt{75}\))2
=>100=AB2+75
=>AB2=25
=>AB=5(cm)
b)Ta có: AB=5cm (chứng minh trên)
BC=10cm (GT)
=>AB= 1/2 BC
=>Tam giác ABC là tam giác nửa đều
=> góc B=60o và góc C=30o (tính chất tam giác nửa đều)

a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.

Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |

Trong toán học, định lý Pytago (còn gọi là định lý Pythagoras theo tiếng Anh) là một liên hệ trong hình học phẳng giữa ba cạnh tam giác của một tam giác vuông.
Đảo lại: Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.
Định lý pytago là vô cùng quan trọng trong giải quyết các bài toán hình học thcs và hình học không gian thpt.

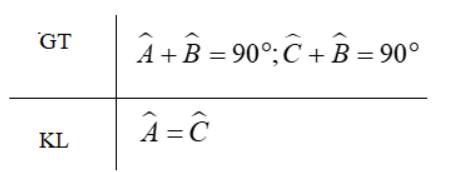
Giả sử \(\widehat A,\widehat C\) cùng phụ với \(\widehat B\). Ta được:
\(\widehat A + \widehat B = 90^\circ ;\widehat C + \widehat B = 90^\circ \)
\(\widehat A = 90^\circ - \widehat B;\widehat C = 90^\circ - \widehat B\)
\( \Rightarrow \widehat A = \widehat C\) (đpcm)
\(KM^2+KN^2=MN^2\)
ta có MK2+NK2=MN2