Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn cần có hình minh họa, hoặc có chi tiết bổ sung thêm vào đề để làm bài này!

Sửa đề: Chiều dài từ gốc cây đến chỗ cây bị gãy là 3m
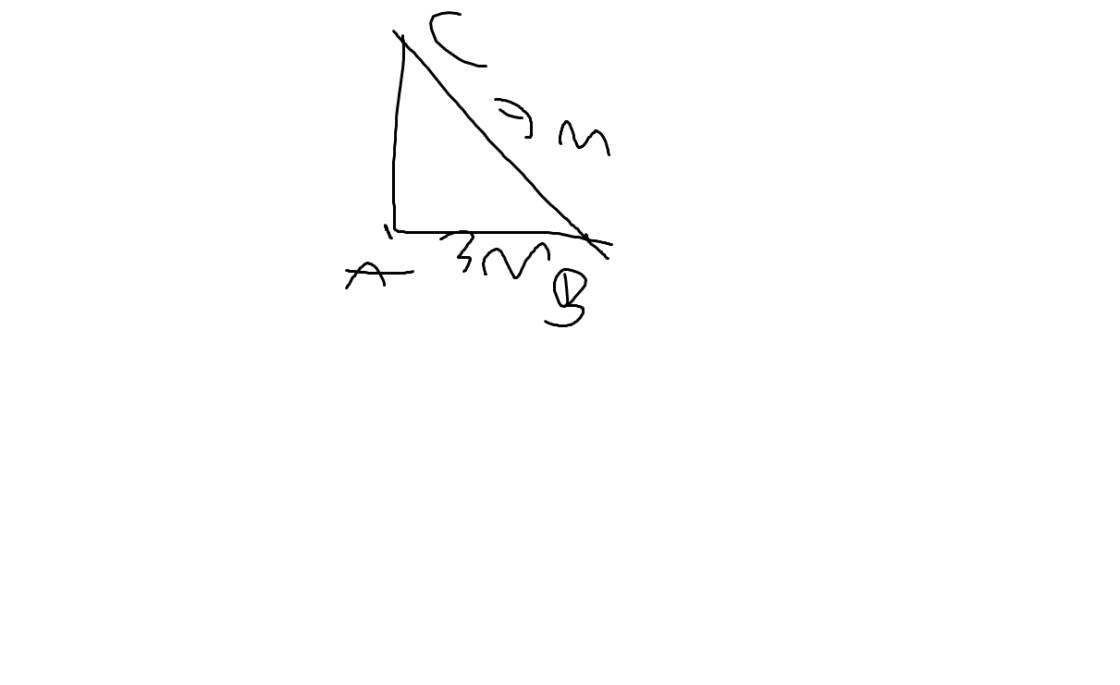
Gọi A là gốc của cái cây
Gọi Clà ngọn của cái cây
Gọi B là chỗ cây bị gãy
Do đó, ta có: \(AB\perp AC\)
Theo đề, ta có: BC=7m; AB=3m
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{7^2-3^2}=2\sqrt{10}\left(m\right)\simeq6,3\left(m\right)\)

Bài 3:
Góc tạo bởi tia sáng với mặt đất là $\alpha$
Ta có:
$\tan \alpha=\frac{7}{4}\Rightarrow \alpha=60,26^0$

Lời giải:
a) Ta có:
{ME∥ACAB⊥AC⇒ME⊥AB⇒∠MEA=900{ME∥ACAB⊥AC⇒ME⊥AB⇒∠MEA=900
{MF∥ABAB⊥AC⇒MF⊥AC⇒∠MFA=900{MF∥ABAB⊥AC⇒MF⊥AC⇒∠MFA=900
Tam giác ABCABC vuông tại AA nên ∠EAF=900∠EAF=900
Tứ giác AFMEAFME có 3 góc ∠MEA=∠MFA=∠EAF=900∠MEA=∠MFA=∠EAF=900 nên là hình chữ nhật.
b)
Vì ME∥AC,MF∥ABME∥AC,MF∥AB nên áp dụng định lý Thales ta có:
MEAC=BMBC;MFAB=CMBCMEAC=BMBC;MFAB=CMBC
Chia hai vế: ⇒MEMF.ABAC=BMCM⇒MEMF.ABAC=BMCM
Vì AFMEAFME là hình chữ nhật (cmt) nên để nó là hình vuông cần có ME=MFME=MF
⇔MEMF=1⇔ABAC=BMCM⇔MEMF=1⇔ABAC=BMCM
⇔ABAB+AC=BMBM+CM=BMBC⇔ABAB+AC=BMBM+CM=BMBC
Vậy điểm M nằm trên BC sao cho BMBC=ABAB+ACBMBC=ABAB+AC thì AFMEAFME là hình vuông.