Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\lim\limits_{x\rightarrow+\infty}x\left(\frac{\left(\sqrt{x^2+2x}+x\right)^2-4\left(x^2+x\right)}{\sqrt{x^2+2x}+x+2\sqrt{x^2+x}}\right)\)
\(=\lim\limits_{x\rightarrow+\infty}2x^2\left(\frac{\sqrt{x^2+2x}-x-1}{\sqrt{x^2+2x}+x+2\sqrt{x^2+x}}\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\frac{2x^2\left(x^2+2x-\left(x+1\right)^2\right)}{\left(\sqrt{x^2+2x}+x+2\sqrt{x^2+x}\right)\left(\sqrt{x^2+2x}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow+\infty}\frac{-2x^2}{\left(\sqrt{x^2+2x}+x+2\sqrt{x^2+x}\right)\left(\sqrt{x^2+2x}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow+\infty}\frac{-2x^2}{x^2\left(\sqrt{1+\frac{2}{x}}+1+2\sqrt{1+\frac{1}{x}}\right)\left(\sqrt{1+\frac{2}{x}}+1+\frac{1}{x}\right)}=\frac{-2}{\left(1+1+2\right)\left(1+1+0\right)}=-\frac{1}{4}\)

\(\lim\limits_{x\rightarrow-\infty}\frac{-2x^5+x^4-3}{3x^2-7}=\lim\limits_{x\rightarrow-\infty}\frac{-2x^3+x-\frac{3}{x^2}}{3-\frac{7}{x^2}}=-\frac{2}{3}.\left(-\infty\right)=+\infty\)
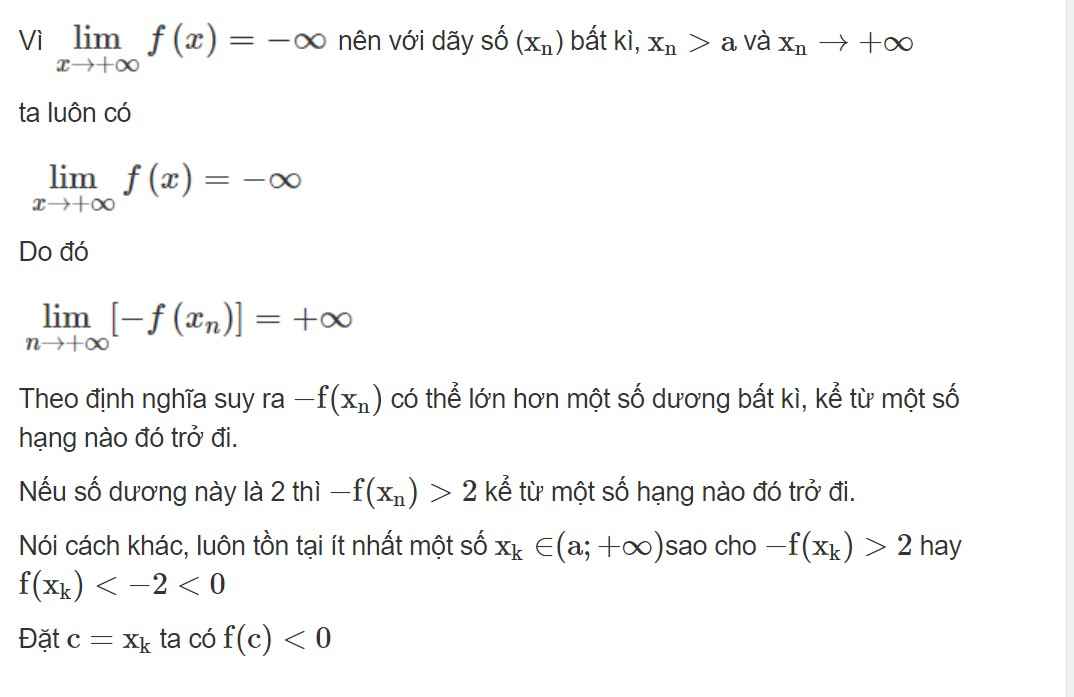
è làm đúng rồi đó bạn
bạn thông minh quá è ơi