

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đầu tiên coi các quả là khác nhau. Do vậy có 9! cách chia.
Nhưng các quả cùng loại (táo, cam, chuối) là giống nhau nên nếu các cháu có cùng loại quả đổi cho nhau thì vẫn chỉ là một cách chia. Vì vậy, số cách chia là:
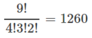
Có thể giải theo các cách như sau:
Chọn 4 trong 9 cháu để phát táo. Có 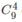 cách.
cách.
Chọn 3 trong 5 cháu còn lại để phát cam. Có 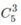 cách.
cách.
Chuối sẽ phát cho 2 cháu còn lại.
Vậy có 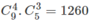 cách.
cách.

1) Xếp 2 quả mít và bưởi:
a) Nếu quả mít ở 3 vị trí đầu hoặc 3 vị trí cuối thì mỗi cách xếp quả mít cho ta 1 cách xếp quả bưởi cách quả mít đúng 2 quả.
b) Nếu quả mít ở vị trí từ 4 đến 7; thì với mỗi cách xếp quả mít cho ta 2 cách xếp vị trí quả bưởi. Khi đó có 4.2=8 cách xếp 2 quả mít; bưởi
Theo quy tắc cộng; có 3+3+8=14 cách xếp 2 quả mít; bưởi.
2) Xếp 8 quả còn lại vào 8 vị trí còn lại:; có 8! Cách xếp.
Vậy số cách xếp cần tìm: 8!. 14 = 564480.
Chọn C.

a) Trong trường hợp này, số cách đặt bằng số các nghiệm \(\left(x_1,x_2,x_3\right)\) nguyên, không âm của phương trình \(x_1+x_2+x_3=3\). Từ đó, đáp số cần tìm là \(C^2_5=10\)
b) Quả thứ nhất có 3 cách đặt
Quả thứ hai có 3 cách đặt
Quả thứ ba có 3 cách đặt
Vậy số cách đặt là \(3^3=27\)

n(Ω)= C102=45
A:” lấy hai quả khác loại” thì n(A)= C51.C31+C51.C21+C21 C31=31.
Vậy P(A)=31/45
Chọn C

b. số cách chọn 2 quả cầu màu đỏ và một quả cầu màu xanh là C42.C51= 30
Chọn A

Chọn B
Đặt 7 quả bóng trên bàn, giữa 7 quả bóng có 6 khoảng trống. Ta muốn chia làm 4 phần thì ta dùng 3cái que, ta đặt vào 3 trong 6 khoảng trống, ta có C 6 3 cách đt.
Do đó số cách chia 7 quả bóng thành 4 phần để bỏ vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả là: C 6 3 = 20 cách

mình cũng nghĩ là có một cách nhưng cô cho đáp án là 105 cách áp dụng công thức tổ hợp