Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Tập xác định D=R\{m}.
Ta có 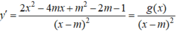
Hàm số đồng biến trên 1 ; + ∞ khi và chỉ khi g x ≥ 0 v à m ≤ 1 (1)
Vì ∆ ' g = 2 ( m + 1 ) 2 ≥ 0 , ∀ m nên (1) tương đương g(x)=0 có hai nghiệm thỏa x 1 ≤ x 2 ≤ 1
Điều kiện tương đương là
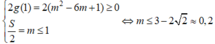
Do đó không có giá trị nguyên dương của m thỏa yêu cầu bài toán.
Chọn D.

\(y'=\dfrac{x-m-x+1}{\left(x-m\right)^2}=\dfrac{1-m}{\left(x-m\right)^2}\)
Hàm số nghịch biến trên khoảng \(\left(-\infty;2\right)\Leftrightarrow y'< 0\forall x\in\left(-\infty;2\right)\Leftrightarrow\left\{{}\begin{matrix}1-m< 0\\x\ne m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ge2\end{matrix}\right.\Rightarrow m\ge2\)
Có 19-2+1=18 giá trị nguyên của m thỏa mãn

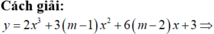
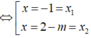

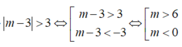

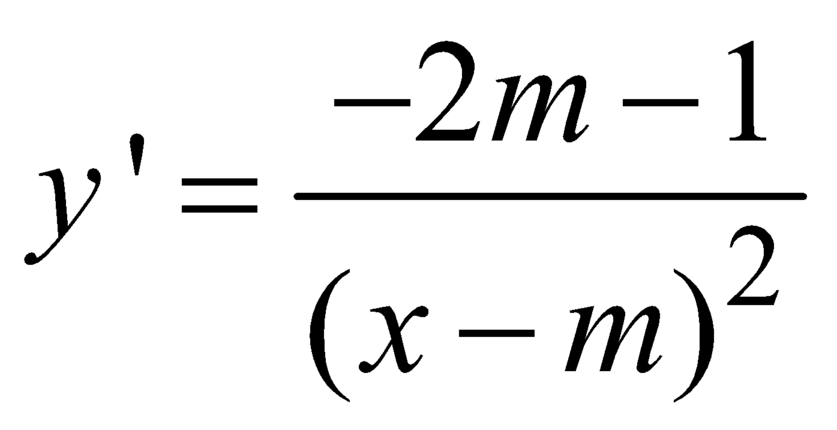
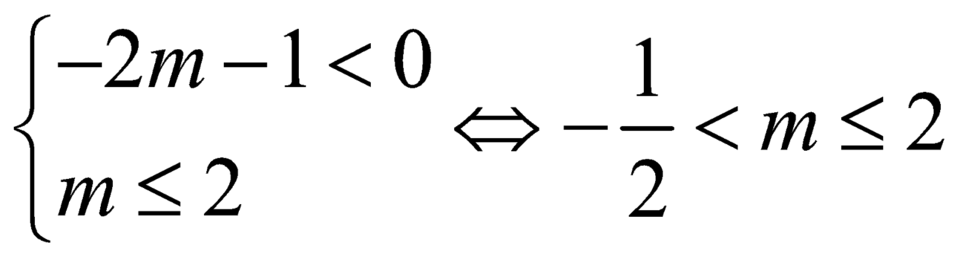


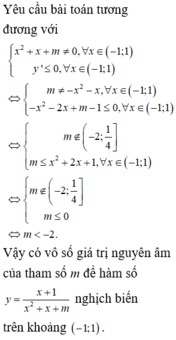

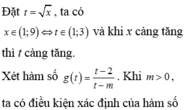


Có \(y'=\dfrac{5x^2+2mx-3m+5}{\left(5x+m\right)^2}\)
Để hàm số đã cho nghịch biến trên \(\left(-3,1\right)\) thì 2 điều kiện sau đồng thời phải được thỏa mãn:
ĐK 1: \(5x^2+2mx-3m+5\le0,\forall x\in\left(-3,1\right)\)
\(\Leftrightarrow\left(2x-3\right)m\le-5x^2-5,\forall x\in\left(-3;1\right)\)
\(\Leftrightarrow m\ge\dfrac{-5x^2-5}{2x-3},\forall x\in\left(-3;1\right)\)
\(\Leftrightarrow m\ge\max\limits_{\left(-3;1\right)}\left(\dfrac{-5x^2-5}{2x-3}\right)\)
Xét \(f\left(x\right)=\dfrac{-5x^2-5}{2x-3}\) trên \(\left(-3;1\right)\)
Ta có \(f'\left(x\right)=\dfrac{-10x^2+30x+10}{\left(2x-3\right)^2}\)
\(f'\left(x\right)=0\Leftrightarrow-10x^2+30x+10=0\) \(\Leftrightarrow x^2-3x-1=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{13}}{2}\left(loại\right)\\x=\dfrac{3-\sqrt{13}}{2}\left(nhận\right)\end{matrix}\right.\)
BBT:
Dựa vào BBT, ta thấy \(\max\limits_{\left(-3;1\right)}f\left(x\right)=10\). Do vậy \(m\ge10\)
ĐK 2: phương trình \(5x+m=0\Leftrightarrow m=-5x\) vô nghiệm trên \(\left(-3,1\right)\)
Khi đó xét \(g\left(x\right)=-5x\), hiển hiên \(g\left(x\right)\) nghịch biến trên \(\left(-3,1\right)\)
\(\Rightarrow g\left(1\right)< g\left(x\right)< g\left(-3\right)\) \(\Leftrightarrow-5< g\left(x\right)< 15\)
Vậy \(\left[{}\begin{matrix}m\le-5\\m\ge15\end{matrix}\right.\)
Kết hợp với ĐK 1, ta có \(m\ge15\)
Mà \(m\inℤ^+,m\le2024\) nên \(m\in\left\{15,16,17,...,2024\right\}\)
\(\Rightarrow\) Có tất cả \(2024-15+1=2010\) giá trị m thỏa ycbt.