
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phân tích thành nhân tử
a)x8 +14x4 +1 b) x8 +98x4 +1
Thích thì bài đây


Gửi Thắng Nguyễn: Mình không biết tại sao lại ko phân tích được?

e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)

Cách 1 : Nhẩm nghiệm của đa thức
Cách 2 : Dùng sơ đồ hocle
Cách 3 : Dùng hằng đẳng thức
Cách 4 : Liên hợp
Bạn nói cụ thể dùm mình được không? Mình vẫn chưa hiểu. hay bạn cho thêm ví dụ về cách tính đy. Hay ví dụ nào để mình dễ hiểu hơn được không? o0o I am a studious person o0o

Để phân tích đa thức thành nhân tử ta có 4 cách:
1. Dùng phương pháp đặt nhân tử chung: Với phương pháp này, bn phải tìm ra nhân tử chung giữa các hạng tử, sau đó đặt nhân tử chung ra ngoài, phần còn lại của đa thức bn cho vào ngoặc riêng để tạo thành 2 hoặc nhiều thừa số nhân vs nhau.
2. Dùng phương pháp dùng hằng đẳng thức: nếu muốn làm tốt các bài tập này bn phải thuộc 7 hằng đẳng thức trong đại số, sau đó tuỳ bài mà tìm hằng đẳng thức tương ứng để khai triển hoặc thu gọn. Cac hằng đẳng thức thường gặp là hằng đẳng thức số 1,2 và 3.
3. Dùng phương pháp nhóm hạng tử: ta nhóm hạng tử trong các bài tập này để xuất hiện nhân tử chung hoặc hằng đẳng thức, sau đó cứ theo như 2 phương pháp đầu mà giải quyết bài tập nhé.
4. Dùng phối hợp nhiều phương pháp: đây là những dạng bài tập nâng cao hơn, đòi hỏi phải kết hợp nhiều phương pháp, khi làm bài tập này, chúng ta phải ưu tiên cho phương pháp đặt nhân tử chung đầu tiên, sau đó là hằng đẳng thức hoặc nhóm hạng tử.
Chúc bn học tốt! ^^
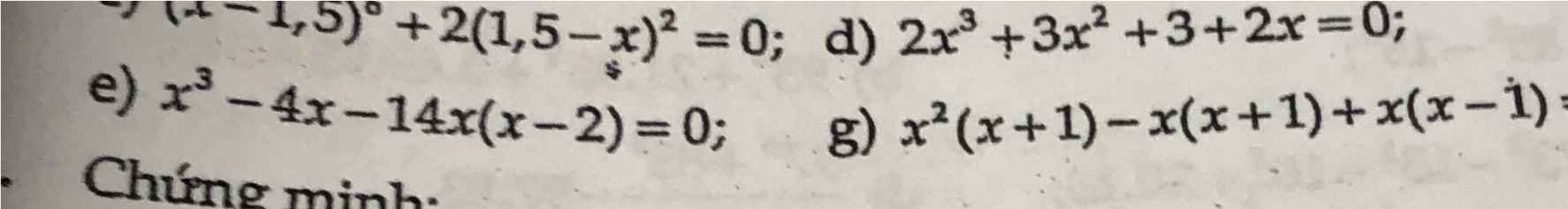
Để làm j vậy bạn ơi?
hỏi chi vậy bạn êy...