Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình
b,Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cân có hai đáy là hai cạnh đối xứng của hình chữ nhật nên hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó
a) Do trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường nên giao điểm của hai đường chéo là tâm đối xứng của hình chữ nhật.
b) Do hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cân có đáy là hai cạnh đối xứng của hình chữ nhật, do đó hai đường thẳng đi qua trung điểm hai cạnh đối của hình chữ nhật là trục đối xứng của hình.

a) Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình.
b) Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cần có đáy là hai cạnh đối xứng của hình chữ nhật là trục đối xứng của hình
a) Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình.
b) Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cần có đáy là hai cạnh đối xứng của hình chữ nhật là trục đối xứng của hình.

a)
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.
Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Vậy: OA = OC và OB= OD
Do đó, O là tâm đối xứng của hình chữ nhật đó.
b)

Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ABCD là hình chữ nhật
⇒ ABCD là hình thang cân (hai đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.
Vậy ta có điều phải chứng minh.

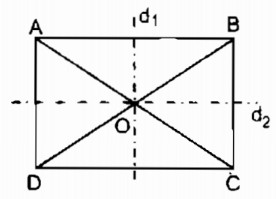
a. Gọi O là giao điểm của hai đường chéo AC và BD.
Vì hình chữ nhật là một hình bình hành nên điểm O là tâm đối xứng của nó.
b. Ta biết trong hình thang cân đường thẳng đi qua trung điểm của hai đáy là trục đối xứng của nó.
Theo định nghĩa ta có hình chữ nhật cũng là một hình thang cân. Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai cạnh đáy AB và CD thì đường thẳng d1d1 đi qua trung điểm của AB và CD là trục đối xứng của hình chữ nhật ABCD.
Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai đáy là AD và BC nên đường thẳng d2d2 đi qua trung điểm của AD và BC là trục đối xứng của hình chữ nhật ABCD.

a,Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình
b,Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cân có hai đáy là hai cạnh đối xứng của hình chữ nhật nên hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó
a,
A B C D O
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.
Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Vậy: OA = OC và OB= OD
Do đó, O là tâm đối xứng của hình chữ nhật đó.
b,
A B C D
Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ABCD là hình chữ nhật
⇒ ABCD là hình thang cân (hai đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD. ( đpcm )

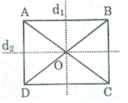
Trong hình thang cân, đường thẳng đi qua trung điểm của hai đáy là trục đối xứng của nó.
Theo định nghĩa ta có hình chữ nhật cũng là một hình thang cân. Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai cạnh đáy AB và CD thì đường thẳng d 1 đi qua trung điểm của AB và CD là trục đối xứng của hình chữ nhật ABCD.
Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai cạnh đáy AD và BC thì đường thẳng d 2 đi qua trung điểm của AD và BC là trục đối xứng của hình chữ nhật ABCD.

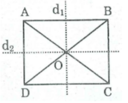
Gọi O là giao điểm hai đường chéo AC và BD.
Vì ABCD là hình chữ nhật nên ABCD cũng là hình bình hành.
Do đó, O là trung điểm của AC và BD.
Suy ra, điểm O là tâm đối xứng của nó.

Do hình chữ nhật là hình bình hành nên nhận giao điểm hai đường chéo làm tâm đối xứng.
Chứng minh
b) Do hình chữ nhật là hình thang cân có đáy là hai cặp cạnh đối của nó. Do đó hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.
XONG RÙI NÀ ^^^^^^^^^^^
~~~ tuong phai cm kieu gt kl co ma`