Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(\overline{a_1a_2a_3a_4a_5a_6}\) là dãy số tự nhiên cần tìm:
ta có \(a_1+a_2+a_3=a_4+a_5+a_6+1\)
mà \(a_1+a_2+a_3+a_4+a_5+a_6=21\)
\(\Rightarrow a_4+a_5+a_6=10\)
các bộ ba số có tổng là 10
\(\left(1,3,6\right);\left(1,4,5\right);\left(2,3,5\right)\)
vì \(a_6\) là số chẵn
\(\Rightarrow\overline{a_4a_5a_6}=2.2.2=8\)
\(\overline{a_1a_2a_3}=3!\)
QTN \(8.3!=48\) số

- Với \(n=4\Rightarrow3^3>4.6\) (đúng)
- Giả sử BĐT đã cho đúng với \(n=k\ge4\) hay \(3^{k-1}>k\left(k+2\right)\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay: \(3^k>\left(k+1\right)\left(k+3\right)\)
Thật vậy, do \(k\ge4\Rightarrow k-3>0\), ta có:
\(3^k=3.3^{k-1}>3k\left(k+2\right)=3k^2+6k=\left(k^2+4k+3\right)+\left(2k^2+2k-3\right)\)
\(=\left(k+1\right)\left(k+3\right)+2k^2+k+\left(k-3\right)>\left(k+1\right)\left(k+3\right)\) (đpcm)

+ sin 2x (x + kπ) = sin (2x + k2π) = sin 2x, (k ∈ Z)
(Do hàm số y = sin x có chu kì 2π).
⇒ Hàm số y = sin 2x tuần hoàn với chu kì π.
+ Hàm số y = sin 2x là hàm số tuần hoàn với chu kì π và là hàm số lẻ.
Bảng biến thiên hàm số y = sin 2x trên [-π/2; π/2]
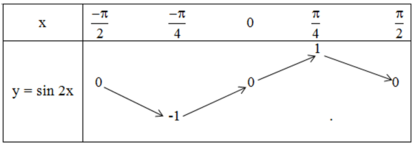
Đồ thị:
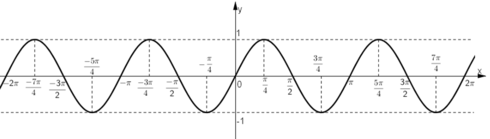
Đồ thị hàm số y = sin 2x.

ĐKXĐ: \(x\ge2\)
\(\Leftrightarrow\left(\sqrt{x-2}\right)^3+m\left(x-2\right)=1\)
Đặt \(\sqrt{x-2}=t\ge0\)
\(\Rightarrow t^3+mt^2=1\Leftrightarrow t^3+mt^2-1=0\)
Đặt \(f\left(t\right)=t^3+mt^2-1\)
Hàm \(f\left(t\right)\) là hàm đa thức nên liên tục trên R
\(f\left(0\right)=-1< 0\)
\(\lim\limits_{t\rightarrow+\infty}f\left(t\right)=\lim\limits_{t\rightarrow+\infty}\left(t^3+mt^2-1\right)=\lim\limits_{t\rightarrow+\infty}t^3\left(1+\dfrac{m}{t}-\dfrac{1}{t^3}\right)=+\infty>0\)
\(\Rightarrow\) Luôn tồn tại 1 giá trị \(t_0>0\) sao cho \(f\left(t_0\right)>0\)
\(\Rightarrow f\left(0\right).f\left(t_0\right)< 0\Rightarrow f\left(t\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;t_0\right)\) hay 1 nghiệm \(t>0\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm \(x=2+t^2>2\)

\(\left(1+\dfrac{1}{n}\right)^n=C_n^0+C_n^1.\dfrac{1}{n}+C_n^2.\dfrac{1}{n^2}+...+C_n^n.\dfrac{1}{n^n}\)
\(=1+1+C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}\)
\(=2+C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}>2\)
Mặt khác:
\(C_n^k.\dfrac{1}{n^k}=\dfrac{n!}{k!\left(n-k\right)!.n^k}=\dfrac{\left(n-k+1\right)\left(n-k+2\right)...n}{n^k}.\dfrac{1}{k!}< \dfrac{n.n...n}{n^k}.\dfrac{1}{k!}=\dfrac{n^k}{n^k}.\dfrac{1}{k!}=\dfrac{1}{k!}\)
\(< \dfrac{1}{k\left(k-1\right)}=\dfrac{1}{k-1}-\dfrac{1}{k}\)
Do đó:
\(C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}=1-\dfrac{1}{n}< 1\)
\(\Rightarrow2+C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}< 2+1=3\) (đpcm)
