Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có : \(m^2+m+1>0\) với mọi m
=> \(\left(m^2+m+1\right)x^4+2x-2=0\)là phương trình bậc 4 với mọi m
Đặt: \(f\left(x\right)=\left(m^2+m+1\right)x^4+2x-2\)
Ta có: \(f\left(0\right)=-2< 0\)với mọi m
\(f\left(1\right)=m^2+m+1>0\) với mọi m
=> Tồn tại \(a\in\left(0;1\right)\) sao cho \(f\left(a\right)=0\) với mọi m
=> Phương trình \(\left(m^2+m+1\right)x^4+2x-2=0\) có nghiệm thuộc ( 0; 1) với mọi m
=> Phương trình \(\left(m^2+m+1\right)x^4+2x-2\)=0 có nghiệm với mọi m.
Ở dòng thứ 6 bạn thêm 1 chút để chặt chẽ hơn:
Vì f(0). f(1) < 0 => tồn tại....

Xét hàm \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)
Hàm \(f\left(x\right)\) là hàm liên tục trên R
\(f\left(1\right)=-2< 0\)
\(f\left(-2\right)=13>0\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)
\(f\left(2\right)=13>0\Rightarrow f\left(1\right).f\left(2\right)< 0\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\)
\(\Rightarrow\) Phương trình đã cho luôn có ít nhất 2 nghiệm với mọi m

(1−m2)(x+1)3+x2−x−3=0
f(x)=(1−m2) (x+1)3+x2−x−3 là hàm đa thức liên tục trên R. Do đó nó liên tục trên [-2; -1]
Ta có f(−1)=−1<0 và f(−2)=m2+2>0 nên f(−1) f(−2)<0 với mọi m.
Do đó, phương trình f(x)=0 luôn có ít nhất một nghiệm trong khoảng (-2; -1) với mọi m. Nghĩa là, phương trình (1−m2) (x+1)3+x2−x−3 luôn có nghiệm với mọi m.
Do hàm số \(\left(1-m^2\right)\left(x+1\right)^3+x^2-x-3\) là hàm đa thức nên nó liên tục trên R, nên liên tục trên \(\left[-2,-1\right]\)
\(f\left(-1\right)=-1< 0;f\left(-2\right)=m^2+2>0\)
\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\)
Do đó phương trình luôn có nghiệm

Đặt \(f\left(x\right)=x^5+x^2-\left(m^2+2\right)x-1\Rightarrow f\left(x\right)\) liên tục trên R
Ta có: \(f\left(0\right)=-1< 0\)
\(f\left(-1\right)=m^2+1>0\) ; \(\forall m\)
\(\Rightarrow f\left(0\right).f\left(-1\right)< 0\) ;\(\forall m\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\) (đpcm)
nếu bài này mà chứng minh có 3 nghiệm thì mình phải làm như thế nào ạ..?

Đặt \(f\left(x\right)=x^5+x^2-\left(m^2+2\right)x-1\)
Hàm \(f\left(x\right)\) liên tục trên R
\(f\left(0\right)=-1< 0\)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\left(x^5+x^2-\left(m^2+2\right)x-1\right)\)
\(=\lim\limits_{x\rightarrow+\infty}x^5\left(1+\dfrac{1}{x^3}-\dfrac{m^2+2}{x^4}-\dfrac{1}{x^5}\right)=+\infty.1=+\infty\)
\(\Rightarrow\) Luôn tồn tại \(a>0\) sao cho \(f\left(a\right)>0\Rightarrow f\left(0\right).f\left(a\right)< 0\Rightarrow\) pt luôn có ít nhất 1 nghiệm thuộc \(\left(0;+\infty\right)\)
\(f\left(-1\right)=m^2+1>0;\forall m\Rightarrow f\left(-1\right).f\left(0\right)< 0\Rightarrow\) pt luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(x^5+x^2-\left(m^2+2\right)x-1\right)=\lim\limits_{x\rightarrow-\infty}x^5\left(1+\dfrac{1}{x^3}-\dfrac{m^2+2}{x^4}-\dfrac{1}{x^5}\right)=-\infty.1=-\infty\)
\(\Rightarrow\) Luôn tồn tại \(b< 0\) sao cho \(f\left(b\right)< 0\Rightarrow f\left(b\right).f\left(-1\right)< 0\Rightarrow\) pt luôn có ít nhất 1 nghiệm thuộc \(\left(-\infty;-1\right)\)
Vậy pt đã cho luôn có ít nhất 3 nghiệm thực

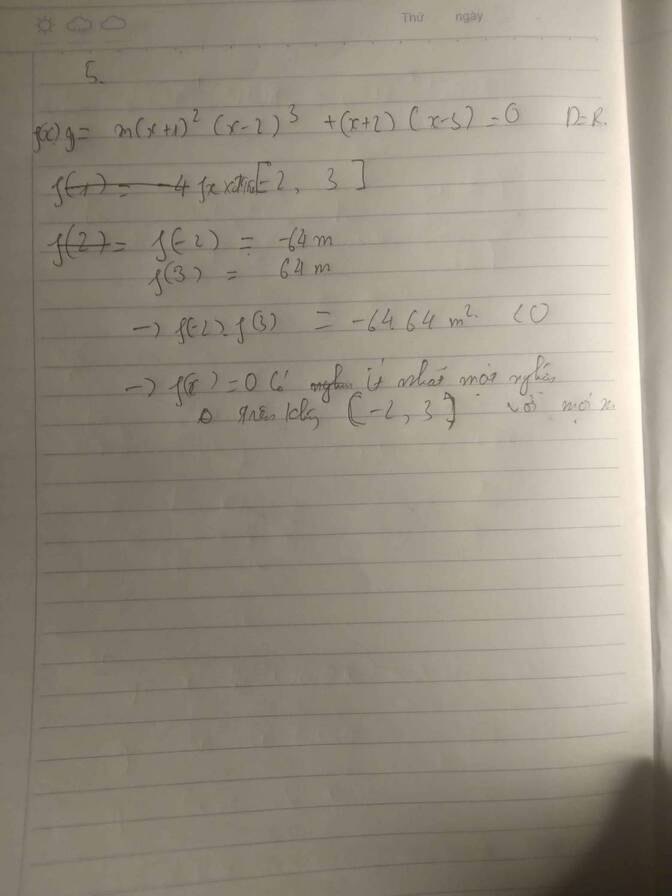
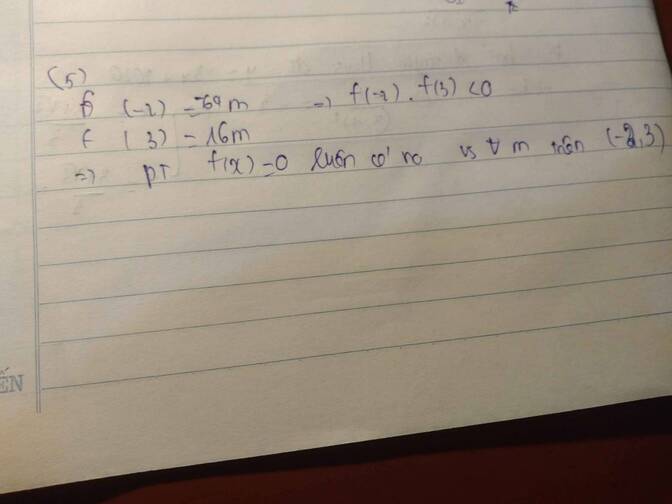
Đặt \(f\left(x\right)=m\left(x-1\right)^{2022}\left(x^2-9\right)+x^2-2\) liên tục trên R
\(\Rightarrow f\left(x\right)\) liên tục trên [-3;1] và [1;3]
\(\Rightarrow\left\{{}\begin{matrix}f\left(1\right)=-1\\f\left(3\right)=7\\f\left(-3\right)=7\end{matrix}\right.\) \(\Rightarrow f\left(1\right)f\left(-3\right)< 0;f\left(3\right).f\left(1\right)< 0\)
\(\Rightarrow\) Tồn tại ít nhất 1 no x \(\in\left(-3;1\right)\) và 1 no x \(\in\) ( 1 ; 3 ) để f(x) = 0 \(\forall m\)
\(\Rightarrow\) p/t có ít nhất 2 no \(\forall m\) (đpcm)