Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải (Giao lưu_cách làm cấp 2)
\(f'\left(x\right)=6x^8-6x^5+6x^2-6x+6=6\left(x^8-x^5+x^2-x+1\right)=6A\)
Cần c/m : \(A>\left(x^8-x^5+x^2-x+1\right)...với\forall x\in R\)
Nếu \(\left|x\right|\ge1\Rightarrow\left\{{}\begin{matrix}x^8\ge x^5\\x^2\ge x\end{matrix}\right.\) \(\Rightarrow A=\left(x^8-x^5\right)+\left(x^2-x\right)+1>0\Rightarrow A>0\)(1)
Nếu \(\left|x\right|< 1\Rightarrow\left\{{}\begin{matrix}x^2>x^5\\1>x\end{matrix}\right.\)\(\Rightarrow A=\left(x^2-x^5\right)+\left(1-x\right)+x^8>0\Rightarrow A>0\)(2)
Từ (1) và (2) \(\Rightarrow A>0\forall x\in R\)=> dpcm

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0

Lời giải:
a) Ta có f'(x) = 3x2 + 1, g(x) = 6x + 1. Do đó
f'(x) > g'(x) <=> 3x2 + 1 > 6x + 1 <=> 3x2 - 6x >0
<=> 3x(x - 2) > 0 <=> x > 2 hoặc x > 0 <=> x ∈ (-∞;0) ∪ (2;+∞).
b) Ta có f'(x) = 6x2 - 2x, g'(x) = 3x2 + x. Do đó
f'(x) > g'(x) <=> 6x2 - 2x > 3x2 + x <=> 3x2 - 3x > 0
<=> 3x(x - 1) > 0 <=> x > 1 hoặc x < 0 <=> x ∈ (-∞;0) ∪ (1;+∞).
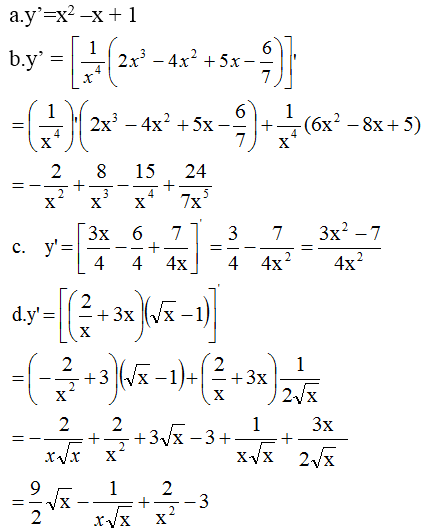
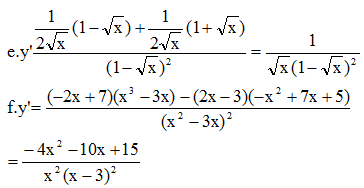
\(f'=6x^8-6x^5+6x+6=6\left(x^8-x^5+x+1\right)\)
\(\left[{}\begin{matrix}\left|x\right|\le1\Rightarrow\left|x^5-x\right|\le\left|x\right|\le1\Rightarrow1-x^5-x\ge0\\\left|x\right|\ge1\Rightarrow\left|x^5\right|\le x^8\Rightarrow\left\{{}\begin{matrix}x^8-x^5>0\\x^2-x>0\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow f'\left(x\right)>0\forall x\)
lập luận 1 noi ,kết luận 1 ngã...ketluan:ngu vai.