Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Xét hai tam giác MNP và MQP có:
\(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\\MP\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta MNP=\Delta MQP\left(c.c.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{NMP}=\widehat{QMP}\\\widehat{NPM}=\widehat{QPM}\end{matrix}\right.\) hay MP là phân giác của góc M và P
b.
Do \(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\end{matrix}\right.\) \(\Rightarrow MP\) là trung trực NQ
\(\Rightarrow MP\perp NQ\) (đpcm)

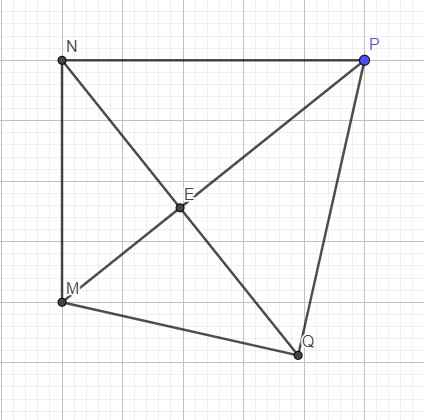
Bài này lạ quá. Hình vẽ là một tứ giác lõm.
Mình hướng dẫn ngắn gọn lời giải
a, Hai tam giác trên bằng nhau theo trường hợp cạnh - cạnh - cạnh
b, Có góc QMN = 80 độ
=> \(\widehat{PMQ}=\widehat{QMN}=\frac{360^o-80^o}{2}=140^o\)
CÓ: \(\widehat{QPM}=\widehat{MPN=\frac{60^o}{2}}=30^o\)
Xét tam giác PMQ biết góc PMQ =140 độ, góc PQM = 30 độ
=> Góc PQM = 10 độ
Mà góc PQM = góc PNM => Góc PNM = 10 độ
d, Xét tam giác QPM cân ở P ( PQ = PN)
=> Đường phân giác PM đồng thời là đường trung trực của đoạn thẳng NQ
e, Xét tam giác PQM có QN là đường trung trực của PM
=> Tam giác PQM cân ỏ Q => QP=PN=QM
Mà QM =MN
=> Tứ giác MNQP có 4 cạnh bằng nhau.

a: Xét ΔMHQ vuông tại H và ΔPKN vuông tại K có
MQ=PN
\(\widehat{MQH}=\widehat{PNK}\)
Do đó: ΔMHQ=ΔPKN
Suy ra: MH=PK

a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân

a: Xét tứ giác MQAP có
MQ//AP
MP//AQ
Do đó: MQAP là hình bình hành

E là TĐ của MQ, F là TĐ của NP
=> EF là đ trung bình của hình thang MNPQ
=> EF//MN
hay ED//MN
mà E là TĐ của MQ
=> D là TĐ của QN
=> ED là đ trung bình của Δ MQN
=> ED=1/2MN(1)
Tương tự: BF=1/2MN(2)
Từ 1 và 2 => ED=BF
=> ED + DB=BF+DB => EB=FD
b,do EF là đ trung bình của hình thang MNPQ
=>\(EF=\dfrac{MN+PQ}{2}\)= \(\dfrac{3+5}{2}\)=4(cm) (3)
Do ED=BF=1/2MN
=> ED=BF=\(\dfrac{3}{2}\)(cm) (4)
Từ 3 và 4 => BD= EF-ED-BF=1(cm)