Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MA+ MB+ 2MC+ 2MD=0
MA+ MA+ AB+ 2MA+ 2AC+ 2MA+ 2AD=0
6MA+ AB+ 2AC+ 2AD=0
6MA+ 2AI+ 4AJ=0
6MA= 2IA+ 4JA
MA= 1/3 IA+ 2/3 JA

a/ \(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AE}\\\overrightarrow{AM}+\overrightarrow{AN}=2\overrightarrow{AE}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AM}+\overrightarrow{AN}\)
b/ \(2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IA}+2\overrightarrow{IE}=2\left(\overrightarrow{IA}+\overrightarrow{IE}\right)=2\overrightarrow{0}=\overrightarrow{0}\)
c/ \(2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=2\left(\overrightarrow{OI}+\overrightarrow{IA}\right)+\overrightarrow{OI}+\overrightarrow{IB}+\overrightarrow{OI}+\overrightarrow{IC}\)
\(=\left(2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+4\overrightarrow{OI}=\overrightarrow{0}+4\overrightarrow{OI}=4\overrightarrow{OI}\)


\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EB} } \right)\\ + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FC} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FD} } \right)\end{array}\)
\( = \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} \overrightarrow { + MG} } \right) + 2\left( {\overrightarrow {GE} + \overrightarrow {GF} } \right) \\+ \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {FC} + \overrightarrow {FD} } \right)\)
\( = 4\overrightarrow {MG} + 2.\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MG} \) (đpcm)

Gọi E, F lần lượt là trung điểm của AM, MB; G, H lần lượt là trung điểm của DN, NC.
Ta có P,Q lần lượt là trung điểm của EG, FH. Khi đó

Đáp án C

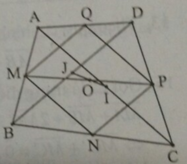
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D

b: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}\)
\(=2\overrightarrow{GE}+2\cdot\overrightarrow{GF}\)
\(=\overrightarrow{0}\)

+) vecto AC + vecto BD = vecto AD + vecto DC + vecto BC + vecto CD
= vecto AD + vecto BC (1)
+) vecto MN = \(\frac{1}{2}\left(\overrightarrow{MD}+\overrightarrow{MC}\right)\)
\(\Leftrightarrow2\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{MB}+\overrightarrow{BC} \)\(=\overrightarrow{AD}+\overrightarrow{BC}\)\(\left(2\right)\)
Từ (1),(2) => đpcm

1) Có \(2\overrightarrow{EF}=\overrightarrow{ED}+\overrightarrow{EC}\)
Lại có : \(\left\{{}\begin{matrix}\overrightarrow{AD}=\overrightarrow{AE}+\overrightarrow{ED}\\\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{EC}\end{matrix}\right.\rightarrow\overrightarrow{AD}+\overrightarrow{BC}=\left(\overrightarrow{AE}+\overrightarrow{BE}\right)+\overrightarrow{ED}+\overrightarrow{EC}=\overrightarrow{0}+\overrightarrow{ED}+\overrightarrow{EC}=\overrightarrow{ED}+\overrightarrow{EC}\) Do đó : \(2\overrightarrow{EF}=\overrightarrow{AD}+\overrightarrow{BC}\left(=\overrightarrow{ED}+\overrightarrow{EC}\right)\)
2) Có : \(\left\{{}\begin{matrix}\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OE}\left(1\right)\\\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OF}=-2\overrightarrow{OE}\left(2\right)\end{matrix}\right.\)
(1) + (2) => \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OE}+2\overrightarrow{OF}=2\overrightarrow{OE}-2\overrightarrow{OE}=\overrightarrow{0}\)
3) \(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)+\overrightarrow{AC}=2\overrightarrow{AC}=4\overrightarrow{AO}\)
4) Ta có : \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=\left(\overrightarrow{MO}+\overrightarrow{OA}\right)+\left(\overrightarrow{MO}+\overrightarrow{OB}\right)+\left(\overrightarrow{MO}+\overrightarrow{OC}\right)+\left(\overrightarrow{MO}+\overrightarrow{OD}\right)=4\overrightarrow{MO}+\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)=4\overrightarrow{MO}+\overrightarrow{0}=4\overrightarrow{MO}\)