Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:
![]()
Trong tam giác vuông ABC vuông tại A có AH là đường cao
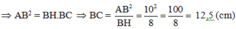
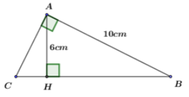
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
![]()
Vậy AC = 7,5 (cm); BC = 12,5 (cm)
Đáp án cần chọn là: B

B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC
AH2=HB x HC =3x4=12
AH=căn 12 r tính mấy cạnh kia đi
B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4
Thế vào cong thức Pytago Tam giác ABC tính máy cái kia

a, AB = 7,5cm, AC = 10cm, BC = 12,5cm, HC = 8cm
b, AH = 3 3 cm; P A B C = 18 + 6 3 c m ; P A B H = 9 + 3 3 c m ; P A C H = 9 + 9 3 c m

bạn tự vẽ hình giúp mik nha
\(AH=\sqrt{AB^2-BH^2}\left(pytago\right)=\sqrt{6^2-3^2}=3\sqrt{3}\)
trong \(\Delta ABC\) vuông tại A có
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{\left(3\sqrt{3}\right)^2}{3}=9\)
\(AC=\sqrt{AH^2+HC^2}=\sqrt{\left(3\sqrt{3}\right)^2+9^2}=6\sqrt{3}\)
chu vi \(\Delta ABC\)
=AB+BC+AC=6+12+6\(\sqrt{3}\)=28,4
chu vi \(\Delta ABH\)
=AB+BH+AH=6+3+3\(\sqrt{3}\)=14,2
chu vi \(\Delta AHC\)
=AH+HC+AC=3\(\sqrt{3}\)+9+\(6\sqrt{3}\)=24,6

A B C 30o 9 H 18 D
a, ^B = ^A - ^C = 900 - 300 = 600
\(\cos B=\frac{AB}{AC}\Rightarrow\frac{1}{2}=\frac{9}{AC}\Rightarrow AC=18\)cm
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=81+324=405\Rightarrow BC=9\sqrt{5}\)cm
b, \(\cos B=\frac{BH}{AB}\Rightarrow\frac{1}{2}=\frac{BH}{9}\Rightarrow BH=\frac{9}{2}\)cm
\(\sin B=\frac{AH}{AB}\Rightarrow\frac{\sqrt{3}}{2}=\frac{AH}{9}\Rightarrow AH=\frac{9\sqrt{3}}{2}\)cm
c, Vì AD là đường phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{DC+BD}{AC+AB}=\frac{9\sqrt{5}}{27}=\frac{\sqrt{5}}{3}\)
\(\Rightarrow BD=\frac{\sqrt{5}}{3}AB=\frac{\sqrt{5}}{3}.9=3\sqrt{5}\)cm
\(\Rightarrow HD=BD-BH=3\sqrt{5}-\frac{9}{2}\)cm
Áp dụng định lí tam giác AHD vuông tại H ta có :
\(AD^2=AH^2+HD^2=\left(\frac{9\sqrt{3}}{2}\right)^2+\left(3\sqrt{5}-\frac{9}{2}\right)^2\)
tự giải nhé ><
a. Giải tam giác ABC
B=60^0
AC=AB/tan30=9.√ 3
BC=AB/sin30=9.2 =18
S=AC.AB/2=81√ 3/2
b. Kẻ AH là đường cao, tính AH, BH
AH=2S/BC=81√ 3/18=9√ 3/2
BH=√ (AB^2-AH^2)=9√ (1-3/4)=9/2