Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

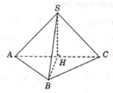
A B C H O P E F M N U V V' K S T L J G I
Gọi EN giao FM tại K, AP cắt BC tại V, AK cắt BC tại U. Giao điểm của EF với AK và AP lần lượt là L và I.
Áp dụng ĐL Thales ta dễ có \(\frac{FL}{AM}=\frac{KF}{KM}=\frac{EF}{MN}=\frac{EI}{AM}\Rightarrow FL=EI\). Từ đây BU = CV
Suy ra hai điểm U,V đối xứng với nhau qua trung điểm T của cạnh BC (1)
Mặt khác gọi S là chân đường cao xuất phát từ A của tam giác ABC. KJ vuông góc AH tại J, AH cắt EF tại G.
Ta thấy ^KJH = ^KEH = ^KFH = 900 nên năm điểm E,F,K,H,J đồng viên
Từ đó \(GE.GF=GH.GJ\Rightarrow\frac{1}{4}SB.SC=\frac{1}{4}SH.SA=GH.GJ\)
Hay \(d_{\left(O,EF\right)}.AG=GH.d_{\left(K,EF\right)}\Rightarrow\frac{d_{\left(O,EF\right)}}{d_{\left(K,EF\right)}}=\frac{GH}{AG}\). Từ đó dễ suy ra L,O,H thẳng hàng
Gọi cát tuyến LOH cắt BC tại V'. Ta lại có CF và OH cắt nhau tại trọng tâm tam giác ABC nên theo ĐL Thales:
\(CV'=2.FL=BU\). Suy ra hai điểm U và V' đối xứng nhau qua trung điểm cạnh BC (2)
Từ (1) và (2) suy ra V trùng V'. Mà AP cắt BC tại V, OH (Đường Euler của tam giác ABC) cắt BC tại V'
Nên OH,AP,BC đồng quy (đpcm).

Câu 3:
a: AB/AC=BD/CD=3/5
=>HB/HC=9/25
b: BC=BD+CD=36+60=96cm
HB/HC=9/25 nên 25HB-9HC=0 và HB+HC=96
=>HB=432/17cm; HC=1200/17cm
\(AH=\sqrt{\dfrac{432}{17}\cdot\dfrac{1200}{17}}=\dfrac{720}{17}\left(cm\right)\)
Bài 1:
AB/AC=2/3 nên HB/HC=4/9
=>HB=4/9HC
Ta có: \(AH^2=HB\cdot HC\)
=>\(HC^2\cdot\dfrac{4}{9}=36\)
=>HC=9(cm)
=>HB=4cm
BC=BH+CH=13cm
\(AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right)\)
\(AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\)


a) Xét tam giác ABF có AE là phân giác đồng thời là đường cao nên nó là tam giác cân tại B.
Vây thì BA = BF.
b) Xét tứ giác HDKF có HF song song và bằng DK nên HDKF là hình bình hành.
Vậy nên HD // FK ; HD = FK
Xét tam giác ABC có AB < AC nên \(\widehat{ABC}>\widehat{ACB}\)

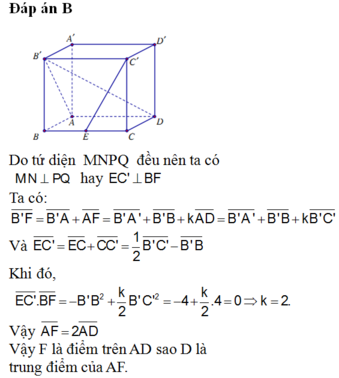
Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
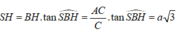
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2