Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ (O;OA) = (O;R/2) dễ thấy ^AMO lớn nhất Khi MA là tiếp tuyến của (O;R/2) <=> tg AMO vuông tại A và sin(^AMOmax) = OA/OM = 1/2 => ^AMOmax = 30o
2/ Gọi O là tâm đường tròn bàng tiếp thuộc ^N . Hạ OH _|_ NM ; OI _|_ NP; OK _|_ MP
Đặt x = MH = MK; y = PI = PK; r = OH = OI = OK
Dễ thấy MK + PK = MP = V(3^2 + 4^2) = 5 <=> x + y = 5 (1)
và NH = NI <=> MN + MH = NP + PI <=> x + 3 = y + 4 <=> x - y = 1 (2)
Giải hệ gồm (1) và (2) => x = 3
Dễ thấy tg HNO vuông cân tại H => r = OH = NH = MN + MH = 3 + 3 = 6cm

đường tròn bàng tiếp học rồi mà bạn nhưng mình không hiểu lắm

b: \(\widehat{NMH}+\widehat{N}=90^0\)
\(\widehat{P}+\widehat{N}=90^0\)
Do đó: \(\widehat{NMH}=\widehat{P}\)
Cho tam giác ABC vuông tại A có AB = 3 ; AC = 4 . TÍnh bán kính đường tròn bàng tiếp nằm trong góc A

A B C O H I K
Gọi (O) là đường tròn bàng tiếp tam giác nằm trong góc A; và H; I; K theo thứ tự là chân đường vuông góc hạ từ O xuống AB; BC; CA
Có: AH; AK là 2 tiếp tuyến đến đường tròn (O) => AH = AK (tính chất tiếp tuyến)
tương tự, BH = BI; CK = CI
Áp dụng ĐL Pi ta go trong tam giác vuông ABC có BC2 = AB2 + AC2 = 25 => BC = 5
=> BI + IC = 5 => BH + CK = 5 (1)
Lại có: AH = AB + BH ; AK = AC + CK mà AH = AK
=> AB + BH + AC + CK => BH - CK = AC - AB = 4 -3 = 1 (2)
Từ (1)(2) => BH = (1 + 5): 2 = 3
Từ giác AHOK có góc HAK = AKO = AHO = 90o và AH = AK
=> AHOK là hình vuông => AH = OH mà AH = AB + BH = 3 + 3 = 6
=> OH = 6
vậy bán kính đương tròn bàng tiếp = 6

Ta có:
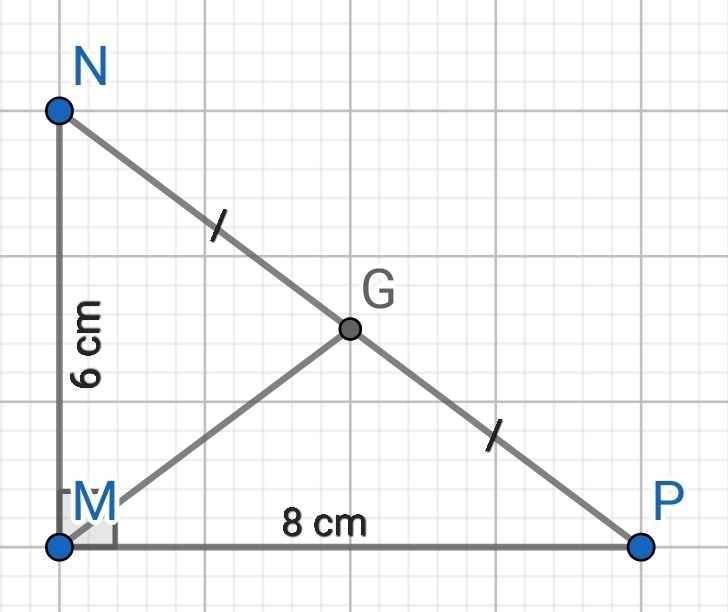
∆MNP vuông tại M
⇒ NP² = MP² + MN² (Pytago)
= 8² + 6² = 100
⇒ NP = 10 (cm)
Gọi G là trung điểm của NP
⇒ MG là đường trung tuyến ứng với cạnh huyền NP của ∆MNP
⇒ MG = NG = PG = NP : 2 = 5 (cm)
⇒ M, N, P cùng thuộc đường tròn tâm G, bán kính MG = 5 cm
Stshdtgfdrsgettgstgefdfe📱📱📱📱📱📱💻📱📱📱📱📱📱📱📱💻💻💻💻💻💻📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱🖍️🖍️📱📱📱📱📱📱📱📱📱📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱📱💻💻📱💻📱💻📱💻📱📱💻💻📱📱💻📱💻📱💻📱💻📱📱💻📱📱📱📱📱📱📱💻📱💻📱📱💻📱📱📱💻📱💻📱📱📱📱📱📱💻💻💻💻📱📱📱📱

a) Xét (O) có
ΔNDP nội tiếp đường tròn(N,D,P∈(O))
NP là đường kính của (O)(gt)
Do đó: ΔNDP vuông tại D(Định lí)
⇒ND⊥DP tại D
hay ND⊥MP(đpcm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔNMP vuông tại N có ND là đường cao ứng với cạnh huyền MP, ta được:
MN2=MD⋅MPMN2=MD⋅MP(đpcm)
b) Vì N,E∈(O) và N,O,E không thẳng hàng
nên NE là dây của (O)
Xét (O) có
OM là một phần đường kính
NE là dây(cmt)
OM⊥NE tại H(gt)
Do đó: H là trung điểm của NE(Định lí đường kính vuông góc với dây)(đpcm)
Theo Py Ta Go tính đc MP = 5
Gọi đường tròn bàng tiếp góc N là O ; từ O kẻ OH vg MP ; OK vg MN ; OI vg NP
=> MH = MK ; HP = PI =>
Cmnp = MN + MP + NP = 3 + 4 + 5 = 12
=> MN + MP + MH + HP = 12
=> MN + MP + MK + PI = 12
=> NK + NI = 12
dễ Cm đc tg OKNI là hv => NK = NI = 6 = OK
=> Bk = 6