Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D K H E I F O
tam giác DEF cân tại D suy ra DE=DF, góc DEF = góc DFE
Xét tam giác KEF và tam giác HFE
có EF chung
góc EKF=góc EHF = 900
góc KEF=góc HFE (CMT)
suy ra tam giác KEF và tam giác HFE (cạnh huyền-góc nhọn)
suy ra EK = HF
mà DK+KE=DE, DH+HF=DF
lại có DE=DF (CMT)
suy ra KD=DH
b) xét tam giác DKO và tam giác DHO
có DO chung
góc DKO = góc DHO = 900
DK = DH (CMT)
suy ra tam giác DKO = tam giác DHO ( cạnh huyền-cạnh góc vuông)
suy ra góc KDO = góc HDO
suy ra DO là tia phân giác của góc EDF (1)
c) Vì DK = DH suy ra tam giác DKH cân tại D
suy ra góc DKH= góc DHK
suy ra góc DKH+ góc DHK + góc KDH = 1800
suy ra góc DKH=(1800 - góc KDH) :2 (2)
Tam giác DEF cân tại D
suy ra góc DEF + góc DFE + góc EDF = 1800
suy ra góc DEF = (1800 - góc KDH) :2 (3)
Từ (2) và (3) suy ra góc DKH = góc DEF
mà góc DKH đồng vị với góc DEF
suy ra KH // EF
d) Xét tam giác DEI và tam giác DFI
có DE = DF (CMT)
DI chung
EI = IF
suy ra tam giác DEI = tam giác DFI (c.c.c)
suy ra góc EDI = góc FDI
suy ra DI là tia phân giác của góc EDF (4)
Từ (1) và (4) suy ra DO trùng DI
hay ba điểm D, O, I thẳng hàng.

Bạn tự vẽ hình nha
a) +)Ta có \(\Delta DEF\)cân tại D (gt) nên DE=DF( suy ra từ khái niệm)
\(\widehat{E}=\widehat{F}\)(suy ra từ tính chất)
+) K là trung điểm của EF (gt) nên KE=KF
+) Xét \(\Delta DEK\) và \(\Delta DFK\)ta có:
DE=DF(cmt)
\(\widehat{E}=\widehat{F}\)(cmt)
KE=KF(cmt)
\(\Rightarrow\Delta DEK=\Delta DFK\left(c.g.c\right)\)
\(\Rightarrow\widehat{DKE}=\widehat{DKF}\)( hai góc tương ứng) (1)
Mặt khác \(\widehat{DKE}+\widehat{DKF}=180\)(2)
Từ (1) và (2) suy ra \(\widehat{DKE}=\widehat{DKF}=\frac{1}{2}180=90\)
\(\Rightarrow DK\perp EF\)(đpcm)
b) +)Vì KE + KF = EF = 24 cm
mà KE = KF (cmt)
\(\Rightarrow KE=KF=\frac{1}{2}24=12\)
+) Áp dụng định lí PYTAGO vào \(\Delta DEK\)vuông tại D có
\(DE^2=DK^2+KE^2\)
\(DK^2=DE^2-KE^2\)
hay\(DK^2=15^2-12^2\)
\(DK=81\)(đpcm)
Vậy chu vi \(\Delta DEK\)là
DE+DK+KE=15+81+12=108(cm)
bn tự vẽ hình nha
a) c1: nếu bn đã học tính chất: trong 1 tam giác cân đường cao đồng thời là phân giác, trung tuyến, trung trực
thì bn lm như sau:
vì k là trung điểm của ef =>dk là trung tuyến của tam giác def
mà tam giác def cân tại d => dk là đường cao của tam giác def
=>dk vuông góc với ef
a) c2 nêu bn chưa học tính chất trên thì bn làm như sau:
xét tam giác dke và tam giác dkf có: cạnh dk chung, de=df( tam giác def cân tại d), ke=kf( k là trung điểm của ef)
=> tam giác dke= tam giác dkf (c.c.c)
=> góc dke= góc dkf( 2 góc tương ứng)[ vt chữ góc lâu quá nên mk ko vt góc bn cx tự hiểu nha)
mà dke+dkf=180 ( 2 góc kề bù) => dke=dkf=90 độ
=> dk vuông góc với ef
b)vì k là trung điểm của ef => ke=kf=ef/2=24/2=12(cm)
vì dk vuông góc với ef (câu a)=> tam giác dke vuông tại k
=>\(de^2=dk^2+ek^2\Rightarrow dk^2=15^2-12^2=81\Rightarrow dk=9\)( vì de>0)
Chu vi tam giác dke là: 15+12+9=36(cm)

a. Xét tam giác ABD và tam giác ACE có:
-AEC=ADB=90 (gt)
-AB=AC (2 cạnh bên tam giác cân ABC)
-A là góc chung
=> tam giác ABD = tam giác ACE (g.c.g) (đpcm)
b.*Vì tam giác ABD = tam giác ACE (câu a)
=> BH=CH (2 cạnh tương ứng)
*Xét tam giác EHB và tam giác DHC có:
-BEH=CDH=90 (gt)
-BH=CH (CM trên)
-EHB=DHC (đối đỉnh)
=> tam giác EHB = tam giác DHC (c.huyền-g.nhọn)
=>EB=DC (2 cạnh tương ứng)
*Ta có: AB=AE+EB
và AC=AD+DC
mà AB=AC (2 cạnh bên tam giác cân ABC)
và EB=DC (CM trên)
=>AE=AD
=> Tam giác ADE cân tại A (đpcm)
c. Vì AE=AD (CM trên)
và HE=HD (CM trên)
=> AH là đường trung trực của ED (đpcm)
d. *Xét tam giác DKC và tam giác DBC có:
-BDC=KDC=90 (gt)
-BD=KD (gt)
-DC là cạnh chung
=>tam giác DKC = tam giác DBC (c.g.c)
=> DBC=DKC (2 góc tương ứng) (1)
*Vì BH=CH (câu b)
=> tam giác HBC cân tại H
=>DBC=ECB (2 góc ở đáy tam giác cân) (2)
*Từ (1) và (2) => ECB=DKC (đpcm)

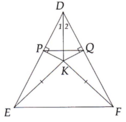
a: Ta có: ΔDEF cân tại D
mà DK là đường trung tuyến
nên DK là đường cao
c: Xét ΔBFK vuông tại K có BF là cạnh huyền
nên FK<FB(1)
Xét ΔDBF có \(\widehat{DBF}>90^0\)
nên FB<FD(2)
Từ (1) và (2) suy ra FK<FB<FD