Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

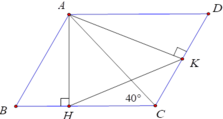
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)

Vì AD.AH = AB.AK ( = S A B C D ) nên A H A K = A B A D = A B B C
Ta lại có AB // CD (vì ABCD là hình bình hành) mà AK ⊥ DC => AK ⊥ AB
=> BAK = 90 ∘ .
Từ đó góc HAK = ABC (cùng phụ với BAH)
Nên ΔAKH ~ ΔBCA (c.g.c) ⇒ A K H ^ = A C B ^ = 40 ∘
Đáp án: B

Xét tam giác AHB và tam giác AKC
^A _ chung ; AB = AC
Vậy tam giác AHB = tam giác AKC (ch-gn)
=> AH/AK = AB/AC => AH/AB = AK/AC
Xét tam giác AKH và tam giác ACB có
^A _ chung; AH/AB = AK/AC
Vậy tam giác AKH ~ tam giác ACB (c.g.c)