Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔCAM cân tại C
=>góc CAM=góc CMA
b: góc HAM+góc CMA=90 độ
góc BAM+góc CAM=90 độ
mà góc CMA=góc CAM
nên góc HAM=góc BAM
=>ĐPCM
c: Xét ΔAHM và ΔANM có
AH=AN
góc HAM=góc NAM
AM chung
=>ΔAHM=ΔANM
=>góc AHM=góc ANM=90 độ
=>MN vuông góc AB

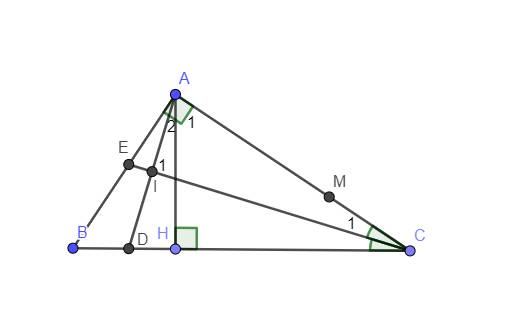
`a)`
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
Lời giải:
a)
$\widehat{B}=\widehat{C}(1)$
$\widehat{AHB}=\widehat{AHC}=90^0(2)$ (do $AH\perp BC$)
$\widehat{B}+\widehat{AHB}+\widehat{BAH}=\widehat{C}+\widehat{AHC}+\widehat{CAH}=180^0(3)$ (tính chất tổng 3 góc trong 1 tam giác)
Từ $(1);(2);(3)\Rightarrow \widehat{BAH}=\widehat{CAH}$ (đpcm)
b)
Vì $\widehat{B}=\widehat{C}$ nên tam giác $ABC$ cân tại $A$
$\Rightarrow $AB=AC$. Mà $AL=AK$ nên $AB-AL=AC-AK$ hay $BL=CK$
Xét tam giác $BKC$ và $CLB$ có:
$BC$ chung
$KC=LB$ (cmt)
$\widehat{B}=\widehat{C}$ (gt)
$\Rightarrow \triangle BKC=\triangle CLB$ (c.g.c)
$\Rightarrow \widehat{BKC}=\widehat{CLB}$
a) Xét ΔABC có \(\widehat{ABC}=\widehat{ACB}\)(gt)
nên ΔABC cân tại A(Định lí đảo của tam giác cân)
hay AB=AC
Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(cmt)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)