Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K I
a)
\(\overrightarrow{AK}=\overrightarrow{AI}+\overrightarrow{IK}=\overrightarrow{AI}+\dfrac{1}{2}\overrightarrow{IB}=\overrightarrow{AI}+\dfrac{1}{2}\left(\overrightarrow{IA}+\overrightarrow{AB}\right)\)
\(=\overrightarrow{AI}+\dfrac{1}{2}\overrightarrow{IA}+\dfrac{1}{2}\overrightarrow{AB}\)\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AI}\).
b) Theo câu a:
\(\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}.\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\).

a) Có \(\overrightarrow{BC}^2=\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{AC}^2+\overrightarrow{AB}^2-2\overrightarrow{AC}.\overrightarrow{AB}\)
Suy ra: \(\overrightarrow{AC}.\overrightarrow{AB}=\dfrac{\overrightarrow{AC^2}+\overrightarrow{AB}^2-\overrightarrow{BC}^2}{2}=\dfrac{8^2+6^2-11^2}{2}=-\dfrac{21}{2}\).
Do \(\overrightarrow{AC}.\overrightarrow{AB}< 0\) nên \(cos\widehat{BAC}< 0\) suy ra góc A là góc tù.
b) Từ câu a suy ra: \(cos\widehat{BAC}=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=-\dfrac{21}{2.6.8}=-\dfrac{7}{32}\).
Do N là trung điểm của AC nên \(AN=AC:2=8:2=4cm\).
\(\overrightarrow{AM}.\overrightarrow{AN}=AM.AN.cos\left(\overrightarrow{AM},\overrightarrow{AN}\right)\)
\(=2.4.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=2.4.\dfrac{-7}{32}=-\dfrac{7}{4}\).

Câu 1:
Gọi E là trung điểm của KC
=>AK=KE=EC
Xét ΔBKC có CM/CB=CE/CK
nên ME//BK
Xét ΔAME có AI/AM=AK/AE
nên IK//ME
=>IK//BK
=>B,I,K thẳng hàng

Lời giải:
Áp dụng các công thức sau: \(|\overrightarrow {a}|^2=\overrightarrow{a}.\overrightarrow{a}\)
\(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{0}\) nếu \(\overrightarrow{a}\perp \overrightarrow{b}\)
Ta có:
\(BC^2.\overrightarrow{IA}+AC^2.\overrightarrow{IB}+AB^2.\overrightarrow{IC}\)
\(=BC^2.\overrightarrow{IA}+AC^2.(\overrightarrow{IA}+\overrightarrow{AB})+AB^2.(\overrightarrow{IA}+\overrightarrow{AC})\)
\(=BC^2.\overrightarrow{IA}+\overrightarrow{IA}(AC^2+AB^2)+AC^2.\overrightarrow{AB}+AB^2.\overrightarrow{AC}\)
\(=2BC^2.\overrightarrow{IA}+AC^2.\overrightarrow{AB}+AB^2.\overrightarrow{AC}\)
\(=\overrightarrow{BC}.\overrightarrow{BC}.\overrightarrow{HA}+\overrightarrow{AC}.\overrightarrow{AC}.\overrightarrow{AB}+\overrightarrow{AB}.\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\overrightarrow {BC}.\overrightarrow{0}+\overrightarrow{AC}.\overrightarrow{0}+\overrightarrow{AB}.\overrightarrow{0}=\overrightarrow {0}\)
Công thức \(\left|\overrightarrow{a}\right|^2=\overrightarrow{a}.\overrightarrow{a}\)và \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{0}\)nếu \(\overrightarrow{a}\perp\overrightarrow{b}\) chứng minh như nào ạ ?
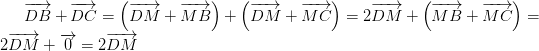
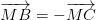
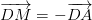
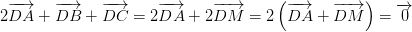
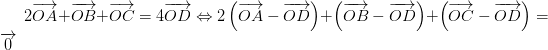
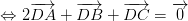 luôn đúng theo câu a
luôn đúng theo câu a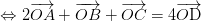 , với O là điểm tùy ý
, với O là điểm tùy ý