Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Xét t, giác ABEC có
M-tđ BC(AM- trung tuyến)
M-tđ AE(E đx A qua M)
BC cắt AE tại M
=> ABEC là hình bình hành (dhnb)
b)Hbh ABEC là hình thoi
<=> AB=AC(dhnb)
Vậy t.giác ABC cân tại A để ABEC là hình thoi
HBH ABEC là hình chữ nhật
<=> A=90 độ (dhnb)
Vậy t.giác ABC vuông tại A để ABEC là hình chữ nhật
Bài 2:
Xét t.giác AKMH có
A=90*
H=90*(MHvg góc AC)
K=90*(MK vg góc AB)
=> AKMH là hình chữ nhật(dhnb)
b) AM là trung tuyến ứng vs cạnh huyền
=> AM=MC
=> tam giác AMC cân tại M
MH là đg cao
=> MH là trung tuyến
=> H - tđ AC
Xét t,giác AMCP có
H- tđ Ac( cmt)
H - tđ MP ( P đx M qua H)
AC cắt MP tại H
=> AMCP là hình bình hành (dhnb)
lại có AM=MC( cmt)
=> AMCP là hình thoi ( dhnb)
Bài 3:
Xét tam giác ABC vg tại A có
AB2 + AC2 = BC2
TS: 52 + 122= BC2
BC2= 25+144
=> BC= 13
Am là trung tuyến
=> AM=1/2BC
=> AM =7,5

a) Xét tứ giác ABEC có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo AE(A và E đối xứng nhau qua M)
Do đó: ABEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành ABEC có \(\widehat{CAB}=90^0\)(ΔABC vuông tại A)
nên ABEC là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Vì D đối xứng với M qua AB(gt)
nên AB là đường trung trực của DM
⇔AB vuông góc với DM tại trung điểm của DM
mà AB cắt DM tại H(gt)
nên H là trung điểm của DM và MH⊥AB tại H
Ta có: MH⊥AB(cmt)
AC⊥AB(ΔABC vuông tại A)
Do đó: MH//AC(Định lí 1 từ vuông góc tới song song)
hay MD//AC
Ta có: H là trung điểm của MD(cmt)
nên \(MH=\dfrac{1}{2}\cdot MD\)(1)
Xét ΔABC có
M là trung điểm của BC(gt)
MH//AC(cmt)
Do đó: H là trung điểm của AB(Định lí 1 đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
H là trung điểm của AB(cmt)
Do đó: MH là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MH=\dfrac{1}{2}\cdot AC\)(Định lí 2 đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra AC=MD
Xét tứ giác ACMD có
AC//MD(cmt)
AC=MD(cmt)
Do đó: ACMD là hình bình hành(Dấu hiệu nhận biết hình bình hành)

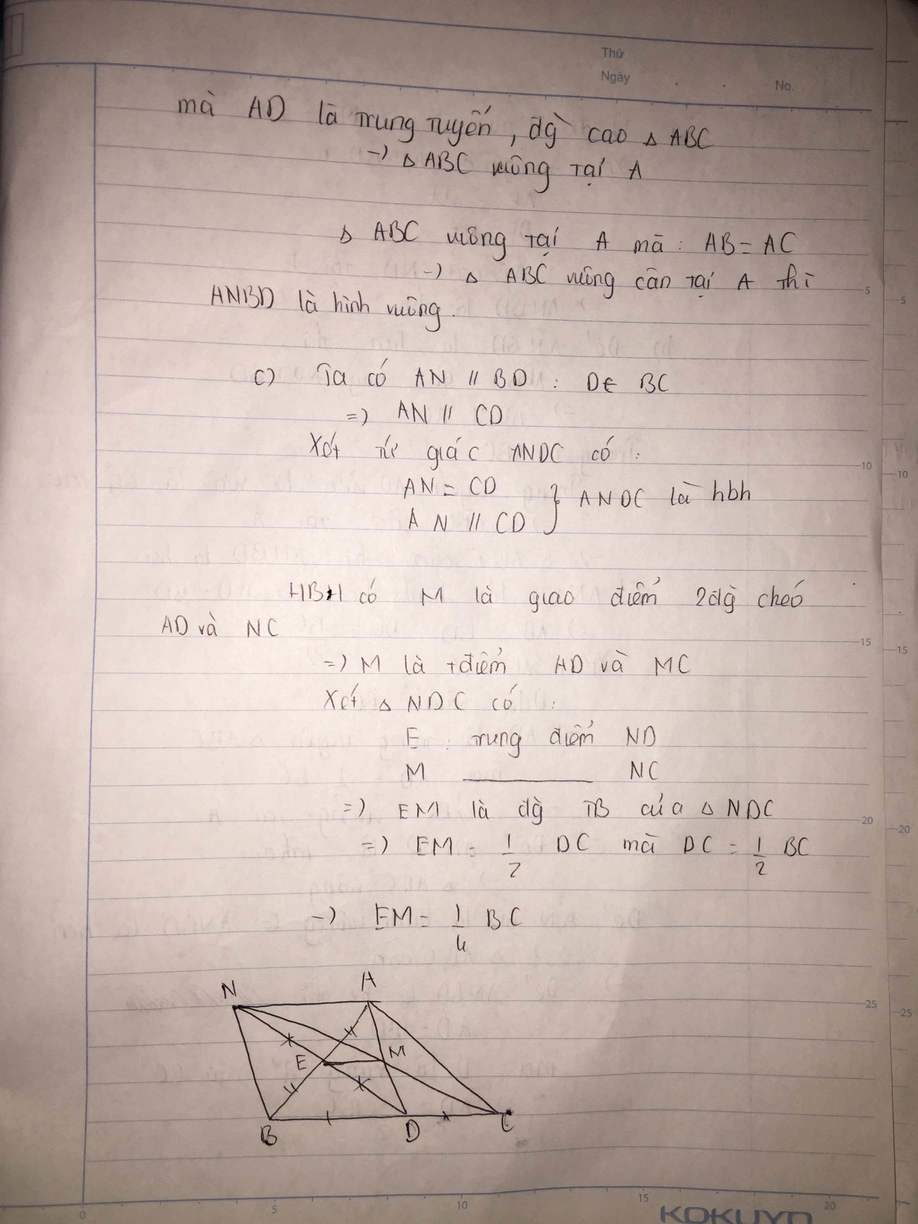
a,Xét tứ giác ABEC có hai đường chéo cắt nhau tại trung điểm mỗi đường
suy ra ABEC là hình bình hành
b,Để ABEC là hình chữ nhật thì góc BAC=90độ suy ra tam giác ABC vuộng tại A thì ABEC là hình chữ nhật
Để ABEC là hình thoi thì AB=AC suy ra tam giác ABC cân tại A thì ABEC là hình thoi
Để ABEC là hình vuông thì góc BAC=90độ và AB=AC suy ra tam giác ABC vuông cân tại A thì ABEC là hình vuông
a, xét abec có
bm=mc, am=me
=> abec là hbh
b hcn:
tam giác abc: có a là góc vuông
có:ab=ac
có: abc vuông cân