Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Trên tia đối của tia EM lấy N sao cho EN=EC
a: Xét ΔABE và ΔAME có
AB=AM
\(\widehat{BAE}=\widehat{MAE}\)
AE chung
Do đó: ΔABE=ΔAME
b: Ta có: ΔABE=ΔAME
=>EB=EM
=>E nằm trên đường trung trực của BM(1)
Ta có: AB=AM
=>A nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AE là đường trung trực của BM
=>AE\(\perp\)BM tại I và I là trung điểm của BM
=>IB=IM
c: Xét ΔENB và ΔECM có
EN=EC
\(\widehat{NEB}=\widehat{CEM}\)(hai góc đối đỉnh)
EB=EM
Do đó: ΔENB=ΔECM
d: Ta có: ΔENB=ΔECM
=>\(\widehat{EBN}=\widehat{EMC}\)
mà \(\widehat{EMC}+\widehat{AME}=180^0\)(hai góc kề bù)
và \(\widehat{AME}=\widehat{ABE}\)(ΔAME=ΔABE)
nên \(\widehat{ABE}+\widehat{NBE}=180^0\)
=>A,B,N thẳng hàng

A B C E D M M
a) Vì AM là phân giác của góc BAC
nên góc BAM = CAM
Xét ΔBAM và ΔCAM có:
AB = AC ( giả thiết )
Góc BAM = CAM ( chứng minh trên )
AM cạnh chung.
=> Δ BAM = ΔCAM ( c.g.c )
=> BM = CM ( 2 cạnh tương ứng )
mà M nằm giữa B và C
Do đó M là trung điểm của BC → ĐPCM.
b) Ta có: AB + BE = AE
AC + CF = AF
mà AB = AC ( đề bài ); AE = AF (đề bài)
=> BE = CF.
Do ΔBAM = ΔCAM nên góc ABC = ACB ( 2 góc tương ứng )
Lại có: Góc ABC + CBE = 180 độ (kề bù)
Góc ACB + BCF = 180 độ (kề bù)
=> ABC + CBE = ACB + BCF
=> Góc CBE = BCF.
Xét ΔBCE và ΔCBF có:
BE = CF ( chứng minh trên)
Góc CBE = BCF ( chứng minh trên)
BC cạnh chung ( theo hình vẽ)
=> ΔBCE = ΔCBF ( c.g.c ) → ĐPCM.
c) Lại do ΔBCE = ΔCBF nên góc EBC = FCB ( 2 góc tương ứng ) hay góc EBM = FCM
Xét ΔMBE và ΔMCF có:
MB = MC ( chứng minh ở câu a )
Góc EBM = FCM ( chứng minh trên)
BE = FC ( chứng minh ở câu b)
=> ΔMBE = ΔMCF ( c.g.c )
=> ME = MF ( 2 cạnh tương ứng ) → ĐPCM.
d) Xét ΔEMN và ΔFMN có:
EM = FM ( chứng minh ở câu c )
EN = FN ( N là trung điểm EF )
MN chung.
=> ΔEMN = ΔFMN.
=> Góc ENM = FNM (2 góc tương ứng)
Suy ra MN là tia phân giác của góc ENF (1)
Có: góc BAM = CAM
Suy ra AM là tia phân giác của góc BAC (2)
Từ (1) và (2) suy ra A, M, N nằm trên cùng 1 đường thẳng.
Do đó A, M, N thẳng hàng → ĐPCM.
A B C M E F N
CM:a) Xét t/giác ABM và ACM
có: AB = AC (gt)
\(\widehat{BAM}=\widehat{CAM}\) (gt)
AM : chung
=> t/giác ABM = t/giác ACM (c.g.c)
=> BM = CM (2 cạnh t/ứng)
=> M là trung điểm của BC
b) Ta có: AE + AC = EC
AF + AB = FB
mà AE = AF (gt); AB = AC (gt)
=> EC = FB
Xét t/giác BCE và t/giác CBF
có: BC : chung
\(\widehat{BCE}=\widehat{FBC}\) (vì t/giác ABC cân)
EC = FB (cmt)
=> t/giác BCE = t/giác CBF (c.g.c)
c) Xét t/giác BEM và t/giác CFM
có: EB = FC (vì t/giác BCE = t/giác CBF)
\(\widehat{EBM}=\widehat{FCM}\) (vì t/giác BCE = t/giác CBF)
BM = CM (cm câu a)
=> t/giác BEM = t/giác CFM (c.g.c)
=> ME = MF (2 cạnh t/ứng)
d) Xét t/giác AEN và t/giác AFN
có: AE = AF (gt)
EN = FN (gt)
AN : chung
=> t/giác AEN = t/giác AFN (c.c.c)
=> \(\widehat{EAN}=\widehat{MAF}\) (2 góc t/ứng)
=> AN là tia p/giác của góc EAF => \(\widehat{EAN}=\widehat{MAF}=\frac{\widehat{EAF}}{2}\)
AM là tia p/giác của góc BAC => \(\widehat{BAM}=\widehat{CAM}=\frac{\widehat{BAC}}{2}\)
Mà \(\widehat{EAF}=\widehat{BAC}\) (đối đỉnh)
=> \(\widehat{EAN}=\widehat{NAF}=\widehat{BAM}=\widehat{MAC}\)
Ta có: \(\widehat{FAN}+\widehat{NAE}+\widehat{EAB}=180^0\)
hay \(\widehat{BAM}+\widehat{EAB}+\widehat{EAN}=180^0\)
=> A, M, N thẳng hàng

A B C E D M
a) Vì AM là phân giác của góc BAC
nên góc BAM = CAM
Xét ΔBAM và ΔCAM có:
AB = AC ( giả thiết )
Góc BAM = CAM ( chứng minh trên )
AM cạnh chung.
=> Δ BAM = ΔCAM ( c.g.c )
=> BM = CM ( 2 cạnh tương ứng )
mà M nằm giữa B và C
Do đó M là trung điểm của BC → ĐPCM.
b) Ta có: AB + BE = AE
AC + CF = AF
mà AB = AC ( đề bài ); AE = AF (đề bài)
=> BE = CF.
Do ΔBAM = ΔCAM nên góc ABC = ACB ( 2 góc tương ứng )
Lại có: Góc ABC + CBE = 180 độ (kề bù)
Góc ACB + BCF = 180 độ (kề bù)
=> ABC + CBE = ACB + BCF
=> Góc CBE = BCF.
Xét ΔBCE và ΔCBF có:
BE = CF ( chứng minh trên)
Góc CBE = BCF ( chứng minh trên)
BC cạnh chung ( theo hình vẽ)
=> ΔBCE = ΔCBF ( c.g.c ) → ĐPCM.
c) Lại do ΔBCE = ΔCBF nên góc EBC = FCB ( 2 góc tương ứng ) hay góc EBM = FCM
Xét ΔMBE và ΔMCF có:
MB = MC ( chứng minh ở câu a )
Góc EBM = FCM ( chứng minh trên)
BE = FC ( chứng minh ở câu b)
=> ΔMBE = ΔMCF ( c.g.c )
=> ME = MF ( 2 cạnh tương ứng ) → ĐPCM.
d) Xét ΔEMN và ΔFMN có:
EM = FM ( chứng minh ở câu c )
EN = FN ( N là trung điểm EF )
MN chung.
=> ΔEMN = ΔFMN.
=> Góc ENM = FNM (2 góc tương ứng)
Suy ra MN là tia phân giác của góc ENF (1)
Có: góc BAM = CAM
Suy ra AM là tia phân giác của góc BAC (2)
Từ (1) và (2) suy ra A, M, N nằm trên cùng 1 đường thẳng.
Do đó A, M, N thẳng hàng → ĐPCM.
Chúc bạn học giỏi nguyễn minh trang!![]()
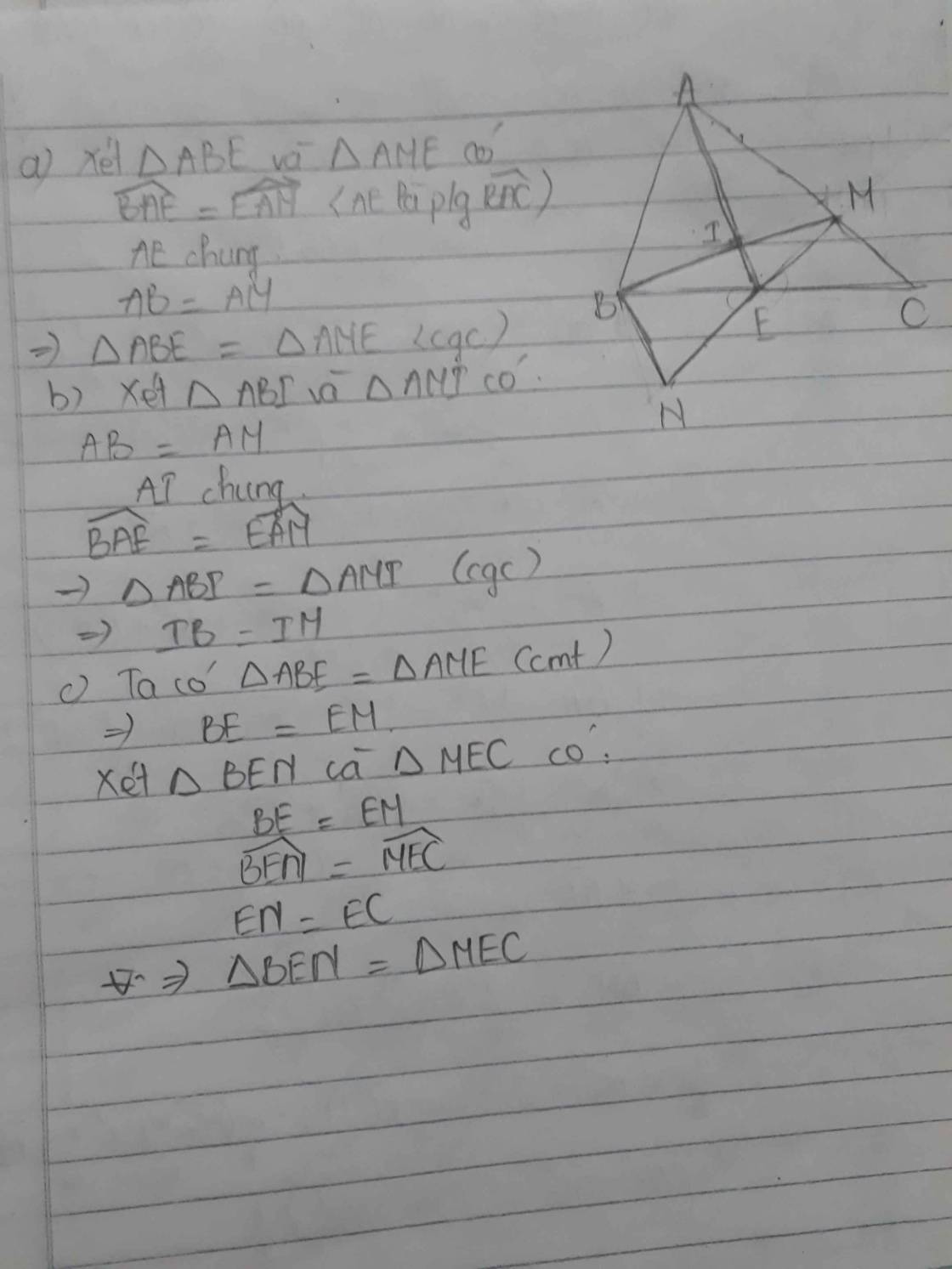
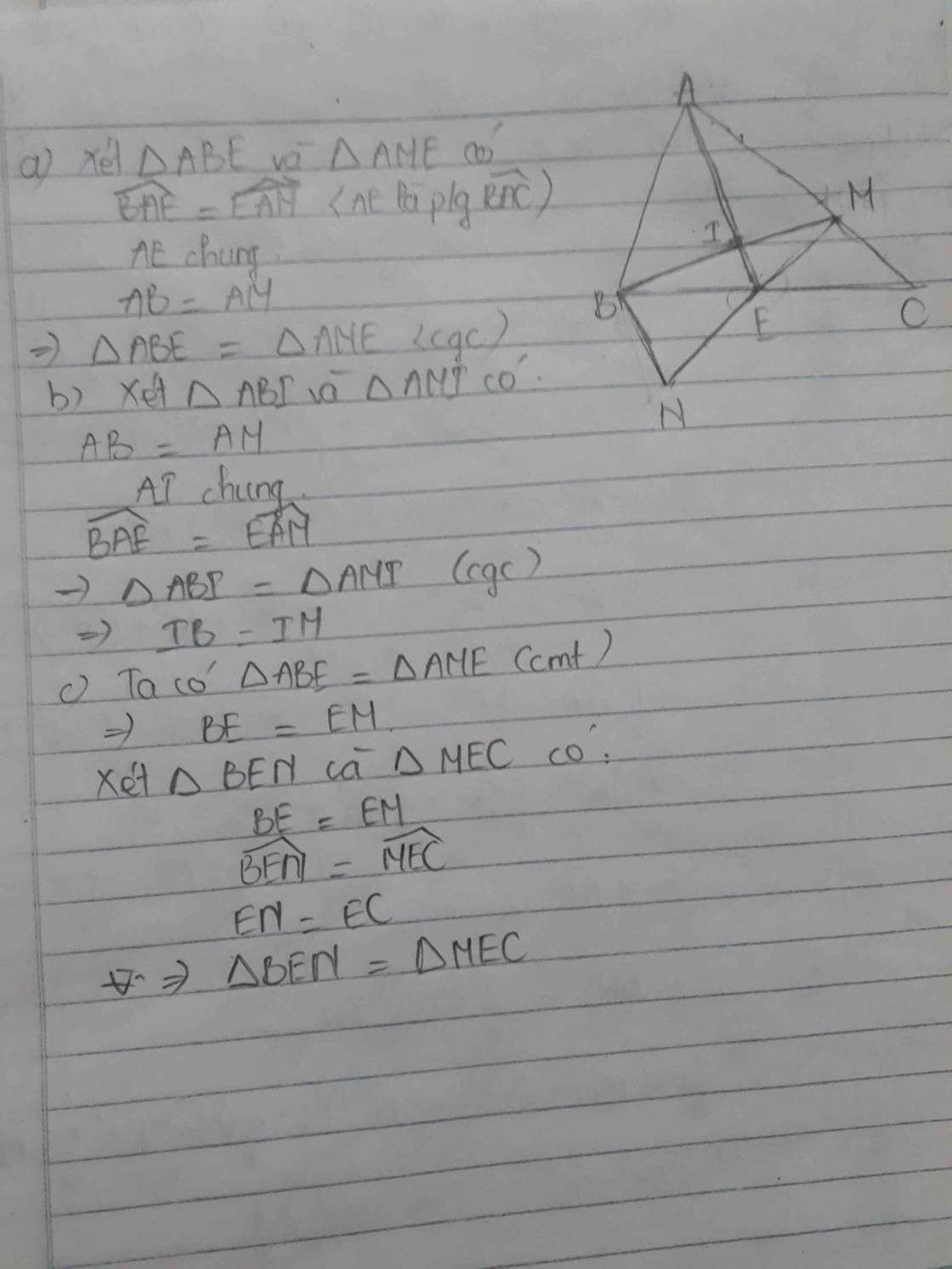
a) xét tam giác ABE và tam giác AME có
AE chung
BAE = EAM(gt)
AB = AM(gt)
=> tam giác ABE = AME (c-g-c)
b)ta có tam giác BAE = EAM(câu a)
=> BE= EM
=>E là trung điểm của BM
(câu c sai đề rồi bạn xem lại nhé!)
d)do góc BNC kề bù với góc CBA => N,B,Athẳng hàng
thanks bạn nhé