Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{6}=\dfrac{CD}{8}\)
mà BD+CD=10cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{6}=\dfrac{CD}{8}=\dfrac{BD+CD}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{30}{7}cm;CD=\dfrac{40}{7}cm\)

b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7
a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC
=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)
b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC2=BC . HC => đpcm
c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm

a, \(\Delta ABC,\hat{BAC}=90^o\)
\(\Rightarrow BC^2=AB^2+AC^2\)(định lý Py-ta-go)
\(\Leftrightarrow10^2=6^2+AC^2\)
\(\Leftrightarrow AC^2=64\)
\(\Leftrightarrow AC=8\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào \(\Delta ABC, \hat{BAC}=90^o, AH\perp BC\) ta có:
\(AB^2=BH.BC\Leftrightarrow6^2=BH.10\Leftrightarrow BH=3,6\left(cm\right)\)
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)\(\Leftrightarrow AH^2=\frac{576}{25}\Leftrightarrow AH=4,8\left(cm\right)\)
Chu vi tam giác ABC: 6 + 10 + 8 = 24 (cm)
Diện tích tam giác ABC: \(\frac{4,8.10}{2}=24\left(cm^2\right)\)

a)Ta có: 62+82=102
⇒ AB2+AC2=BC2
⇒ ΔABC vuông tại A (Py-ta-go đảo)
b)Ta có:\(AB^2=BD.BC\Leftrightarrow BD=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\) (hệ thức lượng)
Ta có: \(AC^2=CD.BC\Leftrightarrow CD=\dfrac{AC^2}{BC}=\dfrac{8^2}{10}=6,4cm\) (HTL)
Ta có: \(AD.BC=AB.AC\Leftrightarrow AD=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8cm\) (HTL)
c)Vì P là hình chiếu của D trên AB
⇒DP⊥AB \(\Rightarrow\widehat{APD}=90^o\)
Xét ΔAPD và ΔADB có:
\(\widehat{A}:chung\)
\(\widehat{APD}=\widehat{ADB}=90^o\)
⇒ ΔAPD ∼ ΔADB (g-g)
\(\Rightarrow\dfrac{AP}{AD}=\dfrac{AD}{AB}\Rightarrow AP.AB=AD^2\) (1)
Chứng minh tương tự,ta có: ΔADQ ∼ ΔACD (g-g)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AQ}{AD}\Rightarrow AC.AQ=AD^2\) (2)
Ta có: AD2 = BD.CD (HTL) (3)
Từ (1)(2)(3)⇒AP.AB=AC.AQ=BD.CD=AD2
d)Xét tg APDQ có: \(\widehat{DPA}=\widehat{PAQ}=\widehat{AQD}=90^o\)
⇒ APDQ là hình chữ nhật
⇒ AD=PQ và \(\widehat{PDQ}=90^o\)
Ta có: AP.BP=DP2 (HTL trong ΔADB)
AQ.CQ=DQ2 (HTL trong ΔADC)
⇒ AP.BP+AQ.CQ=DP2+DQ2=PQ2 (Py-ta-go trong ΔPDQ vuông tại D)
Mà PQ=AD ⇒ AP.BP+AQ.CQ=AD2
e) Ta có: PQ=AD (cmt)
Mà AD = 4,8 cm
⇒ PQ = 4,8 cm

a.
\(AB^2+AC^2=4,5^2+6^2=56,25\)
\(BC^2=7,5^2=56,25\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A theo Pitago đảo
b.
Theo định lý phân giác: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow DB=\dfrac{3}{4}DC\)
Mà \(DB+DC=BC=7,5\)
\(\Rightarrow\dfrac{3}{4}DC+DC=7,5\Rightarrow DC=\dfrac{30}{7}\left(cm\right)\)
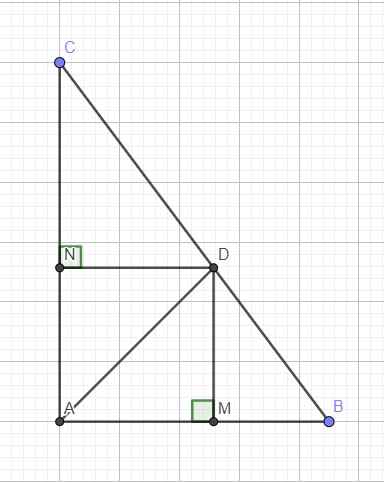
Do DN và AB cùng vuông góc AC \(\Rightarrow DN||AB\)
Áp dụng định lý Talet:
\(\dfrac{DN}{AB}=\dfrac{DC}{BC}=\dfrac{4}{7}\Rightarrow DN=\dfrac{4}{7}AB=\dfrac{18}{7}\left(cm\right)\)
Tứ giác AMDN là hình chữ nhật (có 3 góc vuông)
Mà AD là đường chéo đồng thời là phân giác theo giả thiết
\(\Rightarrow AMDN\) là hình vuông
\(\Rightarrow S_{AMDN}=DN^2=\dfrac{324}{49}\approx6,6\left(cm^2\right)\)