K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

17 tháng 2 2020
Xét \(\Delta\)ABC có DE //BC
=> \(\frac{AD}{AB}=\frac{AE}{AC}\)( ta lét)
=> \(\frac{AC}{AB}=\frac{AE}{AD}=\frac{AC-EC}{AD}=\frac{AC-AD}{AD}\)( vì AD = CE)
=> \(\frac{AC}{AB}=\frac{AC}{AD}-1\)
Khi đó: \(\frac{10}{6}=\frac{10}{AD}-1\)
<=> \(\frac{10}{AD}=\frac{16}{6}\)
<=> AD= 10.6 : 16 = 3,75

30 tháng 3 2020
A E B D C F
Theo Talet có : DE //AC => \(\frac{CD}{CB}=\frac{AE}{AB}\)
: DF // AB => \(\frac{BD}{BC}=\frac{AF}{AC}\)
Giả sử EF // BC => \(\frac{AE}{AB}=\frac{AF}{AC}\Rightarrow\frac{CD}{CB}=\frac{BD}{BC}\)
=> CD = BD
=> D là trung điểm của BC

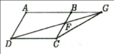
Lời giải:
Vì $EF$ song song với $BC$ nên áp dụng định lý Thales ta có:
\(\frac{AE}{AB}=\frac{AF}{AC}\Leftrightarrow \frac{AE}{5}=\frac{AF}{9}\)
\(\Leftrightarrow 9AE=5AF\)
Mà \(AF=AC-FC=9-FC\)
\(\Rightarrow 9AE=5(9-FC)\)
Khi \(AE=CF\Rightarrow 9AE=5(9-AE)\)
\(\Leftrightarrow 14AE=45\Leftrightarrow AE=\frac{45}{14}\) (cm) \((<5\) cm)
Vậy điểm E nằm trên đoạn thẳng $AB$ sao cho \(AE=\frac{45}{14}\) cm