K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

24 tháng 8 2021
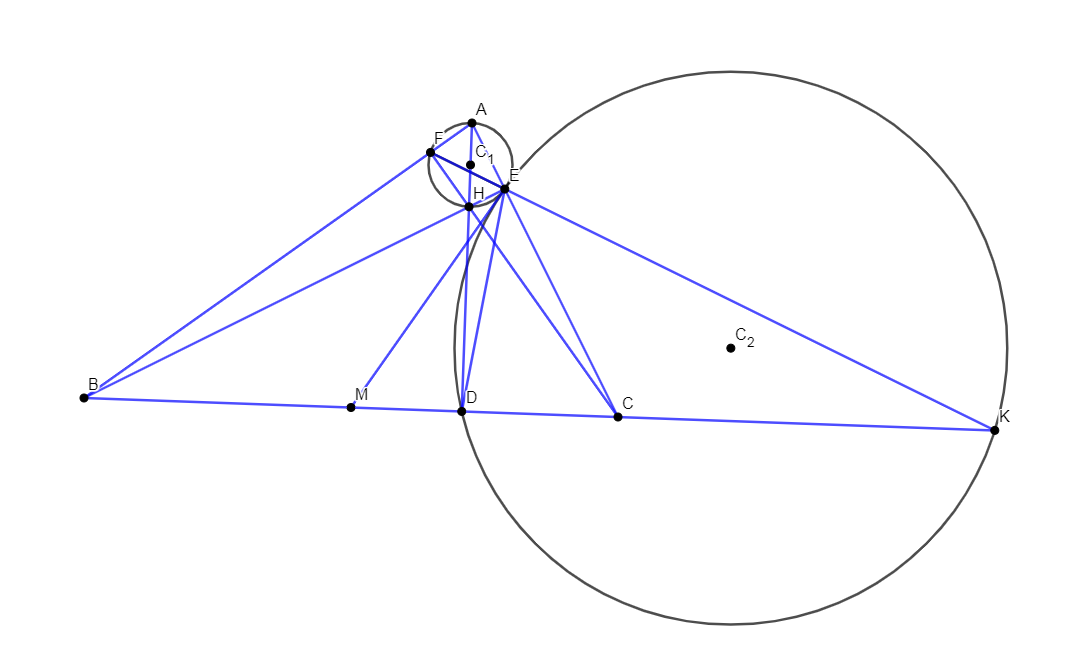
Có \(\Delta ECB\) vuông tại E và có EM là đường trung tuyến
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\)
\(\Rightarrow\Delta EBM\) cân tại M
\(\Rightarrow\widehat{BEM}=\widehat{MBE}\)
mà \(\widehat{MBE}=\widehat{CAD}\) (vì cùng phụ góc BCA)
\(\Rightarrow\widehat{BEM}=\widehat{CAD}\)
\(\Rightarrow\)EM là tiếp tuyến của (C1)
CM tương tự đc EM là tiếp tuyến của (C2)

15 tháng 6 2023
1: góc HEP+góc HKP=180 độ
=>HEPK nội tiếp
2: Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hbh
=>M là trung điểm của HD
Xét ΔAHD có DO/DA=DM/DH
nên OM/AH=DO/DA=1/2