Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho tam giác abc cân tại a và 2 đường trung tuyến bm, cn cắt nhau tại K
a) chứng minh: tam giác bnc = tam giác cmb
b) chứng minh tam giác bkc cân tại K
c) chứng minh BC< 4km

cho tam giac abc can tai a va 2 duong trung tuyen bm,cn cat nhau tai k
a) Cm:tam giac bnc=tam giac cmb
b)Cm:tam giac bkc can tai k
c)Cm:bc<4km
ta có tg ABC cân ở A => AB=AC (t/c)
mà BM,CN là đường Trung tuyến
=> AN=NB , AM = MC
khi đó : BN = \(\dfrac{1}{2}\)AB và MC=\(\dfrac{1}{2}AC\)
=> BN=MC
xét ΔBNC và ΔCMB có
BN =MC (CMT)
\(\widehat{NBC}=\widehat{MCB}\) (t/c tam giác cân )
BC : cạnh chunh
=> ΔBNC = ΔCMB (g.c.g)

Ta có: Tam giác ABC cân tại A => AB = AC
=>AB/2 = AC/2
=> NB=MC
Xét tam giác BNC và tam giác CMB có
NB = MC ( cmt)
góc B = góc C
BC cạnh chung
=> tam giác BNC = tam giác CMB ( cạnh - góc - cạnh )
Mệt quá câu A thôi nha !

 1.
1.
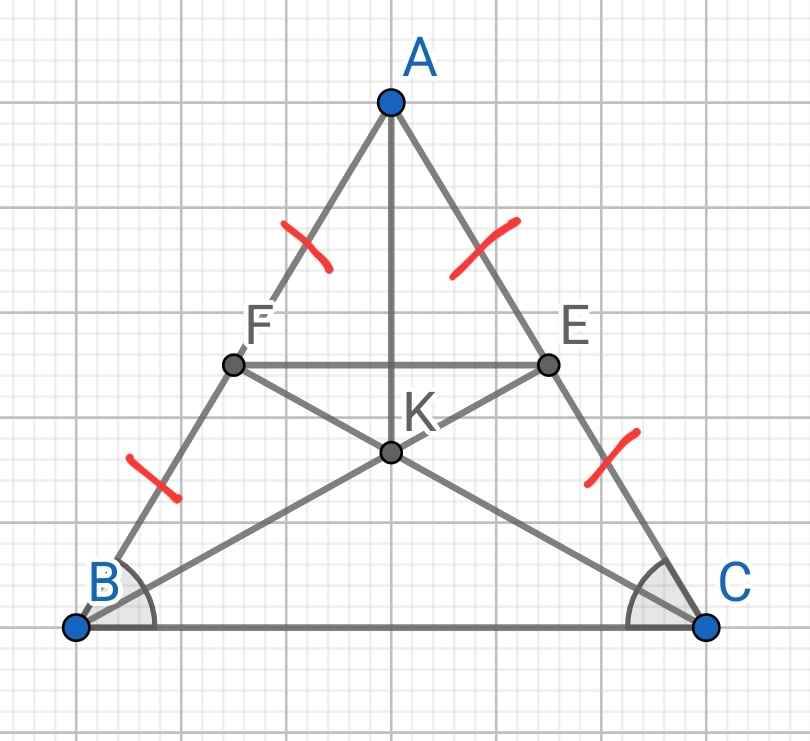
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB (1)
Do BE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AC
⇒ AE = CE = AC/2 (2)
Do CF là đường trung tuyến của ∆ABC (gt)
⇒ F là trung điểm của AB
⇒ AF = BF = AB/2 (3)
Từ (1), (2) và (3) ⇒ BF = CE
Do ∠ABC = ∠ACB (cmt)
⇒ ∠FBC = ∠ECB
Xét ∆BFC và ∆CEB có:
BF = CE (cmt)
∠FBC = ∠ECB (cmt)
BC chung
⇒ ∆BFC = ∆CEB (c-g-c)
⇒ CF = BE (hai cạnh tương ứng)
Hay BE = CF
b) Do ∆BFC = ∆CEB (cmt)
⇒ ∠BCF = ∠CBE (hai góc tương ứng)
⇒ ∠BCK = ∠CBK
∆BKC có:
∠BCK = ∠CBK (cmt)
⇒ ∆BKC cân tại K
c) Do ∆BKC cân tại K (cmt)
⇒ BK = CK
Do ∠ABC = ∠ACB (cmt)
⇒ ∠ABK = ∠ABC - ∠CBK = ∠ACB - ∠BCK = ∠ACK
⇒ ∠FBK = ∠ECK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
∠FBK = ∠CEK (cmt)
BF = CE (cmt)
⇒ ∆BFK = ∆CEK (c-g-c)
⇒ FK = EK (hai cạnh tương ứng)
d) Sửa đề: Chứng minh ∆BFK = ∆CEK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
BF = CE (cmt)
FK = EK (cmt)
⇒ ∆BFK = ∆CEK (c-c-c)
2.
a) Từ (1), (2) và (3) ⇒ AF = AE
∆AEF có:
AE = AF (cmt)
⇒ ∆AEF cân tại A
b) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (4)
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF = (180⁰ - ∠FAE) : 2
⇒ ∠AFE = ∠AEF = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠ABC = ∠AFE
Mà ∠ABC và ∠AFE là hai góc đồng vị
⇒ EF // BC
c) Xét ∆AFK và ∆AEK có:
AF = AE (cmt)
AK chung
FK = EK (cmt)
⇒ ∆AFK = ∆AEK (c-c-c)

a: Xét ΔNBC và ΔMCB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
DO đó: ΔNBC=ΔMCB
Suy ra: \(\widehat{BNC}=\widehat{CMB}\)
b: Xet ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)
nên ΔKBC cân tại K

Tgiac ABC cân tại A => AB = AC và góc ABC = ACB (1)
Ta có: AB = AC, mà M và N lần lượt là trung điểm của AC và AB => AN = NB = AM = MC
Xét tgiac BNC và CMB có:
+ BN = MC
+ BC chung
+ góc NBC = MCB
=> Tgiac BNC = CMB (c-g-c)
Xét tgiac ABM và ACN có:
+ AM = AN
+ AB = AC
+ chung góc A
=> Tgiac ABM = ACN (c-g-c)
=> góc ABM = ACN
(1) => góc ABC - ABM = ACB - ACN
=> góc KBC = KCB
=> Tgiac KBC cân tại K
=> \(\widehat{BKC}=180^o-2.\widehat{KBC}\)(vì góc KBC = KCB)
Tgiac ABC cân tại A, có góc A = 60o => ABC là tgiac đều
Mà M là trung điểm AC => BM là đg cao tgiac ABC
=> góc AMC = 90o
Do tổng 3 góc trong 1 tgiac là 180o
=> góc KBC (MBC) = 180o - 90o - 60o = 30o
Vậy góc BKC = 180o - 2.30o = 120o
a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó: ΔBNC=ΔCMB
b: Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)
nên ΔKBC cân tại K