TH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
29 tháng 6 2017
a, Chứng minh AH là đường trung bình của tam giác BCD
b, Sử dụng hệ thức giữa đường cao và các cạnh góc vuông trong tam giác vuông BCD và áp dụng câu a)
18 tháng 1 2021
A B C D E H O M
a) Từ O kẻ OM vuông góc với AD
Khi đó theo tính chất của đường kính và dây cung thì M là trung điểm AD
Lại có O là trung điểm AE => MO là đường trung bình của tam giác ADE
=> MO // DE , lại có MO // BC (cùng vuông góc với AD)
=> DE // BC
b) Tứ giác ABDC nột tiếp đường tròn (O)
=> \(\widehat{ADB}=\widehat{BCA}\Leftrightarrow90^0-\widehat{ADB}=90^0-\widehat{BCA}\Rightarrow\widehat{CBD}=\widehat{ECB}\)
Lại có từ phần a, BED là hình thang vì có BC // DE
=> BCED là hình thang cân
LM
30 tháng 1 2021
a, Xét ΔADE nội tiếp đường tròn đường kính AE
=> AD ⊥ DE (1)
LẠi có AH ⊥ BC = > AD ⊥ BC (2)
Từ (1) và (2) => DE // BC ( cùng vuông góc với AD) (*)
b, Ta có: Tứ giác ABDC nội tiếp
=> ˆADBADB^= ˆACBACB^
Lại có : ˆCBDCBD^ + ˆADBADB^ = ˆACBACB^ + ˆECBECB^ ( cùng bằng 90 độ)
=> ˆCBDCBD^ = ˆECBECB^ (**)
Từ (*) và (**) => BCED là hình thang cân
10 tháng 8 2016
GIẢI: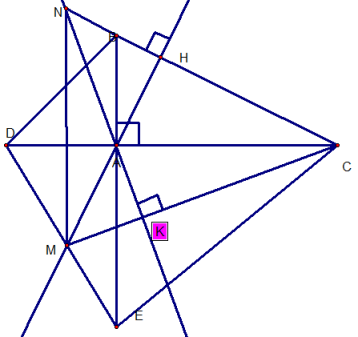
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
30 tháng 8 2015
kẻ 1 đường thẳng vuông góc với BC cắt AC ở E
Xét tam giác CBE vuông tại B có:
1/BK^2=1/BC^2+1/BE^2 (hệ thức lượng)(1)
ta lại có:
*AH vuông góc với BC
BE vuông góc với BC
=>AH//BE (2)
*tam giác ABC cân tại A có:
AH là đường cao của tam gic1 ABC nên:
AH cũng là đường trung tuyến của tam giác ABC
=>H là trung điểm của BC (3)
từ (2) và (3) suy ra:
A là trung điểm của CE (4)
từ (3) và (4) suy ra:
AH là đường trung bình của tam giác CBE
=> AH=BE/2
=>BE=2AH
=>BE2=4AH2 (5)
từ (1) và (5) suy ra:
1/BK^2=1/BC^2+1/4AH^2