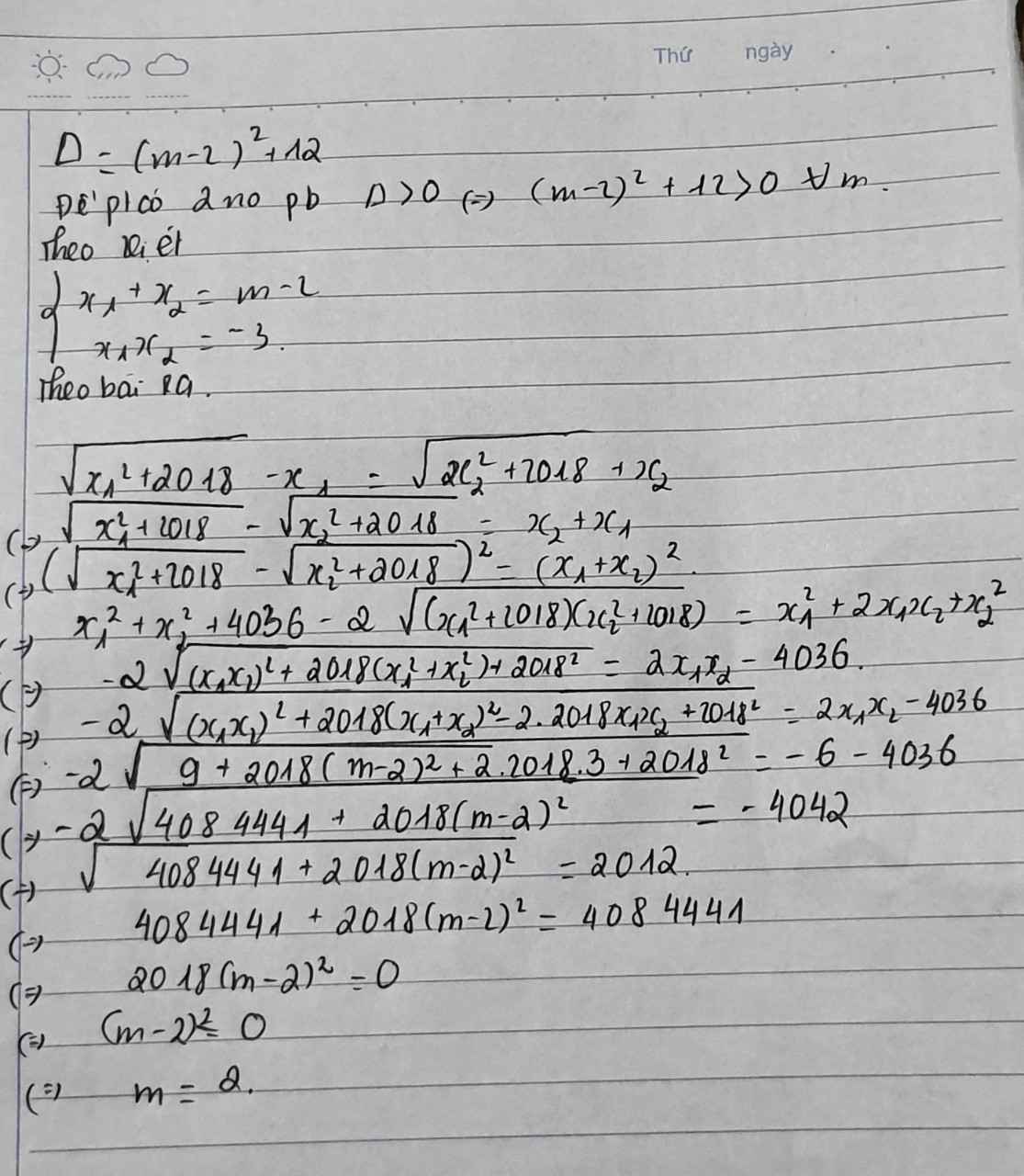Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(x_1x_2=-\frac{2019}{2017}< 0\Rightarrow\) pt có 2 nghiệm trái dấu.
\(\sqrt{x_1^2+2018}-x_2=\sqrt{x_2^2+2018}+x_1\)
\(\Rightarrow x_1^2+x_2^2+2018-2x_2\sqrt{x^2_1+2018}=x_1^2+x_2^2+2018+2x_1\sqrt{x_2^2+2018}\)
\(\Leftrightarrow-x_2\sqrt{x_1^2+2018}=x_1\sqrt{x_2^2+2018}\)
\(\Rightarrow x_2^2\left(x_1^2+2018\right)=x_1^2\left(x_2^2+2018\right)\)
\(\Rightarrow x_1^2=x_2^2\Rightarrow x_1=-x_2\) (do \(x_1;x_2\) trái dấu)
\(\Rightarrow x_1+x_2=0\Rightarrow\frac{m-2018}{2017}=0\Rightarrow m=2018\)

xét pt \(x^2-\left(m-1\right)x-m^2+m-1=0\) \(\left(1\right)\)
từ (1) có \(\Delta=\left[-\left(m-1\right)\right]^2-4.\left(-m^2+m-1\right)\)
\(\Delta=m^2-2m+1+4m^2-4m+4\)
\(\Delta=5m^2-6m+5\)
\(\Delta=5\left(m^2-\frac{6}{5}m+1\right)\)
\(\Delta=5\left[m^2-2.\frac{3}{5}m+\frac{9}{25}-\frac{9}{25}+1\right]\)
\(\Delta=5\left[\left(m-\frac{3}{5}\right)^2+\frac{16}{25}\right]>0\forall m\)
\(\Rightarrow pt\left(1\right)\) luôn có 2 nghiệm phân biệt \(\forall m\)
ta có vi - ét \(\hept{\begin{cases}x_1+x_2=m-1\\x_1.x_2=-m^2+m-1\end{cases}}\)
theo bài ra \(\left|x_2\right|-\left|x_1\right|=2\)
\(\Leftrightarrow\left(\left|x_1\right|+\left|x_2\right|\right)=4\)
\(\Leftrightarrow x_1^2+x_2^2+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow\left(m-1\right)^2-2\left(-m^2+m-1\right)+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow m^2-2m+1+2m^2-2m+2+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow3m^2-4m+3+2\left|x_1.x_2\right|=4\)
cái này đến đây xét ra 2 trường hợp rồi đối chiếu với ĐKXĐ là xong

\(x^2+3x+m-3=0\)
Ta có \(\Delta=b^2-4ac\)
\(=3^2-4.1.\left(m-3\right)\)
\(=9-4m+12\)
\(=21-4m\)
Đẻ pt có 2 nghiệm \(x_1;x_2\)\(\Leftrightarrow\Delta\ge0\Leftrightarrow21-4m\ge0\)
\(\Leftrightarrow x\le\frac{21}{4}\)
Áp dụng vi-ét ta có
\(\hept{\begin{cases}x_1+x_2=-3\\x_1.x_2=m-3\end{cases}}\)
Ta có \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=5\Leftrightarrow\frac{x_1^2+x_2^2}{x_1.x_2}=5\)
\(\Leftrightarrow x_1^2+x_2^2=5x_1x_2\)
\(\Leftrightarrow x_1^2+x_2^2-5x_1.x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-5x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-7x_1x_2=0\)
\(\Leftrightarrow\left(-3\right)^2-7\left(m-3\right)=0\)
\(\Leftrightarrow9-7m+21=0\)
\(\Leftrightarrow30-7m=0\)
\(\Leftrightarrow7m=30\)
\(\Leftrightarrow m=\frac{30}{7}\) (TM)
Vậy \(m=\frac{30}{7}\) thì thỏa mãn bài toán

Bài 1/
a/ Ta có: ∆' = (m - 1)2 + 3 + m
= m2 - m + 4 = \(\frac{15}{4}+\left(x-\frac{1}{2}\right)^2>0\)
Vậy PT luôn có 2 nghiệm phân biệt.
Theo vi et ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3-m\end{cases}}\)
Theo đ
Bài 1/
a/ Ta có: ∆' = (m - 1)2 + 3 + m
= m2 - m + 4 = \(\frac{15}{4}+\left(x-\frac{1}{2}\right)^2>0\)
Vậy PT luôn có 2 nghiệm phân biệt.
Theo vi et ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3-m\end{cases}}\)
Theo đề bài thì
\(x^2_2+x^2_1\ge10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\ge10\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(-3-m\right)\ge0\)
Làm tiếp sẽ ra. Câu còn lại tương tự

Ta có: \(a-b+c=1+2m-2m-1=0\)
Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=-1\\x_2=2m+1\end{matrix}\right.\)
Để biểu thức bài toán xác định thì:
\(\left\{{}\begin{matrix}x_1+x_2=2m\ge0\\3+x_1x_2=2-2m\ge0\end{matrix}\right.\) \(\Rightarrow0\le m\le1\)
\(\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1\)
\(\Leftrightarrow\sqrt{2m}+\sqrt{2-2m}=2m+1\)
\(\Leftrightarrow2m-\sqrt{2m}+1-\sqrt{2-2m}=0\)
\(\Leftrightarrow\frac{4m^2-2m}{2m+\sqrt{2m}}+\frac{2m-1}{1+\sqrt{2-2m}}=0\)
\(\Leftrightarrow\left(2m-1\right)\left(\frac{2m}{2m+\sqrt{2m}}+\frac{1}{1+\sqrt{2-2m}}\right)=0\)
\(\Leftrightarrow2m-1=0\Rightarrow m=\frac{1}{2}\)

\(\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\)
Phương trình luôn có nghiệm thỏa mãn: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
Với \(m\ne1\) ta có:
\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{2018}\Leftrightarrow\frac{x_1+x_2}{x_1x_2}=\frac{x_1+x_2}{2018}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1+x_2=0\\x_1x_2=2018\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m=0\\m-1=2018\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=0\\m=2019\end{matrix}\right.\)

\(\text{Δ}=\left(m+3\right)^2-4m^2\)
\(=m^2+6m+9-4m^2=-3m^2+6m+9\)
\(=-3\left(m^2-2m-3\right)=-3\left(m-3\right)\left(m+1\right)\)
Để phương trình có hai nghiệm phân biệt thì (m-3)(m+1)<0
=>-1<m<3
b:\(\Leftrightarrow x1+x2+2\sqrt{x_1x_2}=5\)
\(\Leftrightarrow m+3+2\sqrt{m^2}=5\)
=>2|m|=5-m-3=2-m
TH1: m>=0
=>2m=2-m
=>3m=2
=>m=2/3(nhận)
TH2: m<0
=>-2m=2-m
=>-2m+m=2
=>m=-2(loại)
c: P(x1)=P(x2)
=>\(x_1^3+a\cdot x_1^2+b=x_2^3+a\cdot x_2^2+b\)
=>\(\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)+a\left(x_1-x_2\right)\left(x_1+x_2\right)=0\)
=>(x1-x2)(x1^2+x1x2+x2^2+ax1+ax2)=0
=>x=0 và a=0
=>\(\left\{{}\begin{matrix}a=0\\b\in R\end{matrix}\right.\)

\(x^2-mx+m-6=0\)
\(\Delta=\left(-m\right)^2-4\left(m-6\right)=m^2-4m+24=\left(m-2\right)^2+20>0\) pt có 2 nghiệm phân biệt
\(\left|x_1-x_2\right|=2\sqrt{5}\)\(\Leftrightarrow\)\(x_1^2+x_2^2-2x_1x_2=20\)\(\Leftrightarrow\)\(\left(x_1+x_2\right)^2-4x_1x_2=20\)
Vi-et ta có : \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-6\end{cases}}\)
(1) \(\Leftrightarrow\)\(m^2-4\left(m-6\right)=20\)\(\Leftrightarrow\)\(\left(m-2\right)^2=0\)\(\Leftrightarrow\)\(m=2\)
...