Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét pt hoành độ gđ của (d) và (P) có:
\(x^2=2x+4m^2-8m+3\)
\(\Leftrightarrow x^2-2x-4m^2+8m-3=0\) (1)
\(\Delta=4-4\left(-4m^2+8m-3\right)\)\(=16m^2-32m+16=16\left(m-1\right)^2\)
Để (P) và (d) cắt nhau tại hai điểm pb khi pt (1) có hai nghiệm phân biệt \(\Leftrightarrow\Delta>0\Leftrightarrow m\ne1\)
Có \(A\in\left(P\right)\Rightarrow y_1=x_1^2\)
\(B\in\left(P\right)\Rightarrow y_2=x_2^2\) , trong đó x1; x2 là hai nghiệm của pt (1)
Theo định lí viet có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-4m^2+8m-3\end{matrix}\right.\)
\(y_1+y_2=10\)
\(\Leftrightarrow x_1^2+x_2^2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(-4m^2+8m-3\right)=10\)
\(\Leftrightarrow8m^2-16m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)(tm)
Vậy...

PTHĐGĐ là:
x^2-(2m+1)x+2m=0
Δ=(2m+1)^2-4*2m
=4m^2+4m+1-8m=(2m-1)^2
Để (P) cắt (d) tại hai điểm phân biệt thì 2m-1<>0
=>m<>1/2
y1+y2-x1x2=1
=>(x1+x2)^2-3x1x2=1
=>(2m+1)^2-3*2m=1
=>4m^2+4m+1-6m-1=0
=>4m^2-2m=0
=>m=0 hoặc m=1/2(loại)

PTHĐGĐ là:
1/2x^2=2x-a+1
=>x^2=4x-2a+2
=>x^2-4x+2a-2=0
Δ=(-4)^2-4(2a-2)
=16-8a+8=-8a+24
Để (d) cắt (P) tại hai điểm phân biệt thì -8a+24>0
=>-8a>-24
=>a<3
x1x2(y1+y2)+48=0
=>(2a-2)*[(x1)^2+(x2)^2]+48=0
\(\Leftrightarrow\left(2a-2\right)\cdot\left[4^2-2\left(2a-2\right)\right]+48=0\)
=>\(\left(2a-2\right)\left(16-4a+4\right)+48=0\)
=>\(\left(2a-2\right)\left(-4a+20\right)+48=0\)
=>\(2\left(a-2\right)\cdot\left(-4\right)\cdot\left(a-5\right)+48=0\)
=>(a-2)(a-5)=-48/-8=6
=>a^2-7a+10-6=0
=>a^2-7a+4=0
=>\(a=\dfrac{7\pm\sqrt{33}}{2}\)

Phương trình hoành độ giao điểm của (P) và d: x 2 − m x + 2 = 0 (1)
P) cắt d tại hai điểm phân biệt A(x1;y1) và B(x2;y2) ⇔ (1) có hai nghiệm phân biệt
⇔ ∆ = m2 – 4.2 > 0 ⇔ m2 > 8 ⇔ m > 2 2 hoặc m<- 2 2
Khi đó x1, x2 là nghiệm của (1). Áp dụng định lí Vi–ét ta có x1 + x2 = m; x1x2 = 2.
Do A, B ∈ d nên y1 = mx1 – 2 và y2 = mx2 – 2.
Ta có:
y 1 + y 2 = 2 ( x 1 + x 1 ) − 1 < = > m x 1 − 2 + m x 2 − 2 = 2 ( x 1 + x 2 ) − 1 < = > ( m − 2 ) ( x 1 + x 2 ) − 3 = 0 < = > m ( m − 2 ) − 3 = 0 < = > m 2 − 2 m − 3 = 0
⇔ m = –1 (loại) hoặc m = 3 (thỏa mãn)
Vậy m = 3 là giá trị cần tìm.
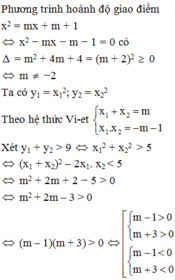
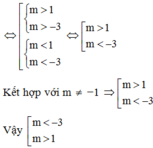

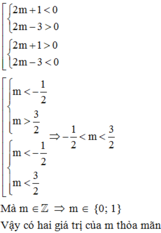
Khi m =3
=> hàm số trở thành y=2x-3+3=2x
Hoành độ giao điểm (p) và (d) là nghiệm pt
\(x^2=2x\)
<=> x2-2x=0
<=> x(x-2)=0
<=> x=0 hoặc x=2
với x=0 thay vào (P) ta có y=02=0
với x=2thay vào (P) ta có y=22=4
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ (0;0)và (2;4) khi m =3
b) Hoành độ giao điểm (p) và (d) là nghiệm pt
\(x^2=2x-m+3\)
\(x^2-2x+m-3=0\)
ta có \(\Delta\)=\(2^2-4\left(m-3\right)\)=\(4-4m+12\)
=\(16-4m\)
Để (p) và (d ) cắt nhau tại 2 điểm phân biệt thì 16-4m>0 hay m<4
Theo Vi ét ta có x1+x2=2
x1.x2=m-3
Và y1=x12; y2=x22
Khi đó x1.x2.( y1+y2)=-6
<=> (m-3) . ( x12+x22)=-6
<=> (m-3). ((x1+x2)2-2x1x2)=-6
<=> (m-3). (4-2m+6)=-6
Tự lm nốt nha bn ! ( mk mỏi tay quá :) ) ( nhớ k mk đấy )