Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

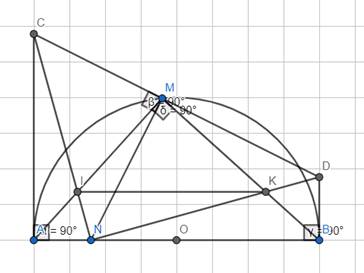
△AMB nội tiếp đường tròn đường kính AB nên △AMB vuông tại M.
- Ta có: \(\widehat{CAB}+\widehat{DBA}=90^0+90^0=180^0\)
\(\Rightarrow\widehat{CAM}+\widehat{MAB}+\widehat{DBM}+\widehat{MBA}=180^0\)
\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+\left(\widehat{MAB}+\widehat{MBA}\right)=180^0\)
\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+90^0=180^0\) nên \(\widehat{CAM}+\widehat{DBM}=90^0\)
Tứ giác ANMC có: \(\widehat{NAC}+\widehat{NMC}=90^0+90^0=180^0\)
Nên tứ giác ANMC nội tiếp \(\Rightarrow\widehat{CAM}=\widehat{CNM}\)
Tứ giác BNMD có: \(\widehat{NBD}+\widehat{NMD}=90^0+90^0=180^0\)
\(\Rightarrow\)Tứ giác BNMD nội tiếp \(\Rightarrow\widehat{MBD}=\widehat{MND}\)
\(\Rightarrow\widehat{CNM}+\widehat{MND}=\widehat{CAM}+\widehat{MBD}=90^0\)
\(\Rightarrow\widehat{INK}=90^0\).
Tứ giác MINK có: \(\widehat{IMK}+\widehat{INK}=90^0+90^0=180^0\)
\(\Rightarrow\)Tứ giác MINK nội tiếp nên \(\widehat{MIK}=\widehat{MNK}\)
Lại có \(\widehat{MNK}=\widehat{MBD}\left(cmt\right)\) \(\Rightarrow\widehat{MIK}=\widehat{MBD}\)
Xét (O): \(\widehat{MBD}=\widehat{MAB}\left(=\dfrac{1}{2}sđ\stackrel\frown{MB}\right)\)
\(\Rightarrow\widehat{MIK}=\widehat{MAB}\) nên IK//AB

1. Vì \(C,D\) nằm trên đường tròn đường kính \(AB\to BD\perp FA,AC\perp BF\to H\) là trực tâm tam giác \(ABF\to FH\perp AB.\)
2. Do tam giác \(ABF\) có \(BD\) vừa là đường cao, vừa là đường phân giác, suy ra \(\Delta ABF\) cân ở \(B.\) Suy ra \(D\) là trung điểm \(FA.\) Vì \(FH\parallel AE\to\frac{DH}{DE}=\frac{DF}{DA}=1\to AEFH\) là hình bình hành. Do hình bình hành này có hai đường chéo vuông góc với nhau nên \(AEFH\) là hình thoi.
3. Vì \(\angle ABC=60^{\circ}\to\Delta ABF\) là tam giác đều, suy ra \(AF=AB=2R\). Mặt khác, \(BD=AB\cdot\cos30^{\circ}=2R\cdot\frac{\sqrt{3}}{2}=R\sqrt{3}.\) Mà \(H\) là trực tâm tam giác đều \(ABF\to HD=\frac{1}{3}BD=\frac{R\sqrt{3}}{3}\to EH=\frac{2R\sqrt{3}}{3}.\)
Vậy diện tích tứ giác \(AEFH\) bằng \(\frac{1}{2}\cdot EH\cdot AF=\frac{1}{2}\cdot\frac{2R\sqrt{3}}{3}\cdot2R=\frac{2R^2\sqrt{3}}{3}.\)