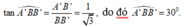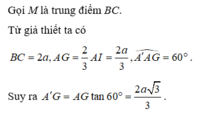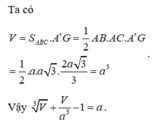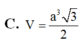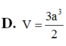Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
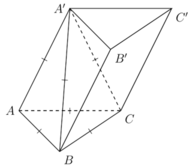
Từ giả thiết suy ra tứ diện A'ABC đều có cạnh a nên có thể tích là
V A ' A B C = a 3 2 12
Khi đó
V A B C . A ' B ' C ' = d A ' , A B C . S A B C = 3 V A ' A B C = a 3 2 4

_ Thể tích khối lăng trụ :
Gọi D là trung điểm của BC ta có : \(BC\perp AD\Rightarrow BC\perp A'D\Rightarrow\widehat{ADA'}=60^0\)
Ta cso \(AA'=AD.\tan\widehat{ADA'}=\frac{3a}{2};S_{ABC}=\frac{a^2\sqrt{3}}{4}\)
Do đó \(V_{ABC.A'B'C'=}S_{ABC}.AA'=\frac{3a^2\sqrt{3}}{8}\)
- Bán kính mặt cầu ngoại tiếp tứ diện GABC :
Ta có I là giao điểm của GH với đường trung trực của AG trong mặt phẳng (AGH)
Gọi E là trung điểm của AG, ta có :
\(R=GI=\frac{GE.GA}{GH}=\frac{GA^2}{2GH}\)
Ta có :
\(GH=\frac{AA'}{3}=\frac{a}{2};AH=\frac{a\sqrt{3}}{3};GA^2=GH^2+AH^2=\frac{7a^2}{12}\)
Do đó \(R=\frac{7a^2}{2.12}.\frac{2}{a}=\frac{7a}{12}\)

Chọn D.
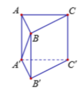
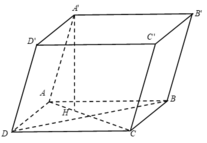
Ta có: ![]() nên BB' là hình chiếu của A'B trên (BCC'B')
nên BB' là hình chiếu của A'B trên (BCC'B')
Vậy góc giữa đường thẳng A'B và mặt phẳng (BCC'B') là góc giữa hai đường thẳng A'B và BB' và là góc A ' B B ' ^
Lại có: