K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 10 2018
Ta có hình vẽ :
A D O B F C E
Xét hình thoi ABCD, E và F là chân đường vuông góc kẻ từ đỉnh A đến các cạnh BC, CD. Xét hai trường hợp :
a) Trường hợp EF = \(\frac{1}{2}\) BD
\(\Delta AEC\)= \(\Delta AFC\) (cạnh huyền và góc nhọn) nên CE = CF.
Tam giác cân CEF có CA là đường phân giác của góc C nên CA
Rồi tới bạn làm nốt
CM
25 tháng 4 2019
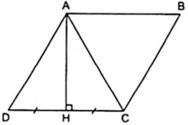
Gọi H là chân đường cao kẻ từ đỉnh A xuống cạnh CD, theo giả thiết ta có:
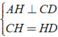⇒ AH là đường trung trực của đoạn CD nên AC = AD ( 1 )
Áp dụng định nghĩa của hình thoi ABCD, ta có
AD = AB = BC = CD ( 2 )
Từ ( 1 ) và ( 2 ) ta có AD = AC = CD ⇒ Δ ACD là tam giác đều
