Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O 58
Vì \(\frac{AC}{BD}=1,05\)
\(\Rightarrow\frac{\frac{1}{2}AC}{\frac{1}{2}BD}=1,05\)
\(\Rightarrow\frac{AO}{BO}=1,05\)
\(\Rightarrow AO=1,05.BO\)
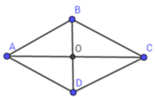
Xét \(\Delta AOB\)vuông tại O ( vì O là giao điểm 2 đường chéo hình thoi ) có :
\(AO^2+BO^2=AB^2\)( Định lý Pytago )
\(\left(1,05.BO\right)^2+BO^2=58^2\)
\(2,1025BO^2=3364\)
\(\Rightarrow BO^2=1600\)
\(\Rightarrow BO=40\) \(\left(BO>0\right)\)
\(\Rightarrow AC=\left(BO.1,05\right).2=84\)(cm)
Vậy ...

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B

Do \(ABCD\) là hình thoi nên hai đường chéo vuông góc với nhau tạo ra 4 góc vuông.
Áp dụng ĐL Pythagore vào 1 trong các tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{6}{2}} \right)}^2} + {{\left( {\frac{8}{2}} \right)}^2}} = \sqrt {9 + 16} = \sqrt {25} = 5\) (cm)

Hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (gt)
⇒O là trung điểm của AC và BD
⇒AO=AC2 và DO=BD2
=> AO=6/2=3(cm) và DO = 8/2= 4cm
AC vuông góc BD TẠI O ( vì ABCD là hình thoi )
tam giác ADO vuông góc tại O có AD bình = AO bình + DO bình ( định lý pytago)
=> AD2 =3 bình + 4 bình = 25 => AD= 5cm
Vậy AB=BC=DC=AD=5cm


có BI//AC gt / CI//BD BOC=90 độ (tcht) suy ra tứ giác OBIC LÀ hình chữ nhật dkpcm
có OBIC là hình chữ nhật suy ra OI=BC (tchcn) mà BC = AB suy ra OIBAB dkpcm
hình thoi abcd cần có 1 góc vuông hình chữ nhất OIBAB là hình vuông

B O C D A 58
Vì : \(\frac{AC}{BD}=1,05\)
\(\Rightarrow\frac{\frac{1}{2}AC}{\frac{1}{2}BD}=1,05\)
\(\Rightarrow\frac{AO}{BO}=1,05\)
\(\Rightarrow AO=1,05.BO\)
Xét \(\Delta AOB\) vuông tại O ( vì O là giao điểm 2 đường chéo của hình thoi )
\(AO^2+BO^2=AB^2\) ( định lí Py ta go )
\(\left(1,05.BO\right)^2+BO^2=58^2\)
\(2,1025BO^2=3364\)
\(\Rightarrow BO^2=1600\)
\(\Rightarrow BO=40\) ( vì \(BO>0\) )
\(\Rightarrow AC=\left(BO.1,05\right).1=84\left(cm\right)\)
Vậy ..............