Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt : \(\overrightarrow{BA}=\overrightarrow{a},\overrightarrow{BB'}=\overrightarrow{b,}\overrightarrow{BC}=\overrightarrow{c}\)
Ta có : \(\overrightarrow{BD'}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Do MM//BD' nên tồn tại số thực k sao cho \(\overrightarrow{MN}=k\overrightarrow{BD'}\)
hay :
\(\overrightarrow{MN}=k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}\) (1)
Đặt
\(\frac{MC}{AC}=x,\frac{C'N}{C'D}=y;x,y\in\left(0;1\right)\)
Ta có :
\(\overrightarrow{AC}=\overrightarrow{c}-\overrightarrow{a,}\overrightarrow{C'D}=\overrightarrow{a}-\overrightarrow{b,}\)
Suy ra : \(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CC'}+\overrightarrow{C'N}\)
\(=\overrightarrow{xAC}+\overrightarrow{CC'}+\overrightarrow{yC'N}\)
\(=x\left(\overrightarrow{c}-\overrightarrow{a}\right)+\overrightarrow{b}+y\left(\overrightarrow{a}-\overrightarrow{b}\right)\)
\(=\left(y-x\right)\overrightarrow{a}+\left(1-y\right)\overrightarrow{b}+x\overrightarrow{c}\) (2)
Từ (1) và (2) suy ra :
\(k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}=\left(y-x\right)\overrightarrow{a}+\left(1-y\right)\overrightarrow{b}+x\overrightarrow{c}\)
\(\Leftrightarrow\left(k+x-y\right)\overrightarrow{a}+\left(k+y-1\right)\overrightarrow{b}+\left(k-x\right)\overrightarrow{c}=\overrightarrow{0}\) (3)
Do \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) không đồng phửng nên (3) tương đương với
\(\begin{cases}k+x-y=0\\k+y-1=0\\k-x=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=\frac{1}{3}=k\\y=\frac{2}{3}\end{cases}\)
Vậy với \(3\overrightarrow{MC}=\overrightarrow{AC,}3\overrightarrow{C'N}=2\overrightarrow{C'D}\)
thì MN//BD' và khi đó \(\frac{MN}{BD'}=\frac{1}{3}\)

NP là đường trung bình của ∆ACD ⇒ NP // AB, mà AB ⊂ (ABC) ⇒NP // (ABC)
P ∈ (MNP) ∩ (ACD) (1)
Trong mặt phẳng (BCD) gọi J = MN ∩ CD, có
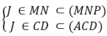
J ∈ (MNP) ∩ (ACD) (2)
Từ (1) và (2) : (MNP) ∩ (ACD) = JP
Trong mặt phẳng (ACD) gọi Q = JP ∩ AC. Có:
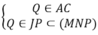
⇒ Q = AC ∩ (MNP). Có:
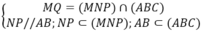
⇒MQ // NP // AB
Theo định lí Ta – lét có
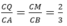
Kết luận:
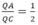
Đáp án A

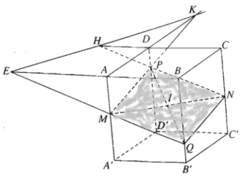
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).

a) Do MN\(\subset\) (BMN); AD \(\subset\)(ABCD) nên I là một điểm chung của (BMN) với (ABCD). Dễ thấy B là một điểm chung khác I
Vậy (BMN)\(\cap\) (ABCD) =BI
b) J\(\in\)BI\(\subset\) (BMN)
J \(\in\) (CD) \(\subset\) (SCD)
nên J là một điểm chung của (BMN) \(\cap\) (SCD)
vậy (SCD) \(\cap\) (BMN) =NJ
Thiết diện của (BMN) với hình chóp là tứ giác AMNJ
c) Áp dụng định lí Menelaus Trong \(\Delta SAD\) có cát tuyến MNI có:
\(\dfrac{ID}{IA}.\dfrac{MA}{MS}.\dfrac{NS}{ND}=1\)
\(\dfrac{ID}{IA}.1.2=1\) => \(\dfrac{ID}{IA}=\dfrac{1}{2}\)
=> D là trung điểm AI
+ Xét tam giác SAI có 2 trung tuyến MI, SD giao nhau tại N => N là trong tâm tam giác SAI
=> \(\dfrac{NI}{MI}=\dfrac{2}{3}\)
Ta có AD//BC
=> \(\dfrac{IK}{BK}=\dfrac{AI}{BC}=\dfrac{2AD}{BC}=2\)(do AD=BC)
=> \(\dfrac{IK}{IB}=\dfrac{2}{3}\)
Xét tam giác MIB có: \(\dfrac{NI}{MI}=\dfrac{IK}{IB}=\dfrac{2}{3}\)
=> BM//NK

Vì MN//BC'D, theo định lí Thales, ta có: AN/NC = AM/MD
Vì AD = 3AM, ta có: MD = AD - AM = 3AM - AM = 2AM
Do đó: AN/NC = AM/MD = AM/2AM = 1/2
Vậy, A'N/NC = 1/2.

a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.

Hic, nghĩ mãi ko thể sử dụng cách dựng hình thông thường được. Phải quay về cách sử dụng vecto mặc dù ghét cách này vì phải tính nhiều (nhưng mà nó dễ :D)
Đặt \(\overrightarrow{BA}=a;\overrightarrow{BC}=\overrightarrow{b};\overrightarrow{BB'}=\overrightarrow{c}\)
Giả sử \(\overrightarrow{AM}=x.\overrightarrow{AC}\) ; \(\overrightarrow{BN}=y.\overrightarrow{BD'}\)
Ta có: \(\overrightarrow{DI}=\overrightarrow{DA}+\overrightarrow{AI}=-\overrightarrow{b}+\dfrac{1}{2}\overrightarrow{c}\)
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}=-x.\overrightarrow{AC}+\overrightarrow{AB}+y.\overrightarrow{BD'}=-x.\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}+y.\left(\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}\right)\)
\(=\left(x+y-1\right)\overrightarrow{BA}+\left(y-x\right)\overrightarrow{BC}+y.\overrightarrow{BB'}=\left(x+y-1\right)\overrightarrow{a}+\left(y-x\right)\overrightarrow{b}+y.\overrightarrow{c}\)
MN và DI song song khi và chỉ khi:
\(\left\{{}\begin{matrix}x+y-1=0\\\dfrac{y-x}{-1}=\dfrac{y}{\dfrac{1}{2}}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\x=3y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y=\dfrac{1}{4}\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy M thuộc đoạn AC sao cho \(AM=\dfrac{3}{4}AC\) \(\Rightarrow\dfrac{AM}{MC}=3\)
N thuộc đoạn BD' sao cho \(BN=\dfrac{1}{4}BD'\)
Phí mất 15ph kẻ kẻ vẽ vẽ dựng dựng, quay qua tính tay bằng vecto mất 30s =))))