Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

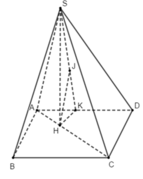
+ Kẻ SH ⊥ AC, H ∈ AC
Do (SAC) ⊥ (ABCD) ⇒ SH ⊥ (ABCD)
+ BD = 2a ⇒ AC = 2a
SA = A C 2 − S C 2 = 2 a 2 − a 3 2 = a ; SH = S A . S C A C = a . a 3 2 a = a 3 2
Ta có: AH = S A 2 − S H 2 = a 2 − a 3 2 2 = a 2 ⇒ AC = 4AH
Lại có: HC ∩ (SAD) = A d C ; S A D d H ; S A D = A C A H = 4
⇒ d(C; (SAD)) = 4d(H; (SAD))
Do BC // (SAD) (BC//AD) ⇒ d(B; (SAD)) = d(C; (SAD))
Do đó d(B; (SAD)) = 4d(H; (SAD))
+ Kẻ HK ⊥ AD tại K, kẻ HJ ⊥ SK tại J
Ta chứng minh được HJ ⊥ (SAD) ⇒ d(H; (SAD)) = HJ
⇒ d(B; (SAD)) = 4HJ
+ Tính HJ
Tam giác AHK vuông tại K có H A K ^ = C A D ^ = 45 ° ⇒ HK = AH.sin 45 ° = a 2 4
Mặt khác: 1 H J 2 = 1 H K 2 + 1 S H 2 ⇒ HJ = a 21 14
Vậy d(B; (SAD)) = 4 . a 21 14 = 2 a 21 7 .
Đáp án C