Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S D A B C H K O
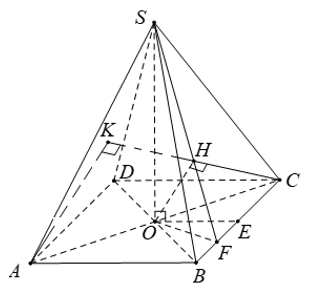
\(\left\{{}\begin{matrix}\left(SBC\right)\perp\left(ABCD\right)\\\left(SBC\right)\cap\left(ABCD\right)=BC\\CD\perp BC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SBC\right)\Rightarrow\alpha=\widehat{DSC}\)
Đặt cạnh đáy là \(x\Rightarrow SD=\frac{x}{sin\alpha}=\frac{x\sqrt{26}}{4}\)
\(\Rightarrow SC=\sqrt{SD^2-CD^2}=\frac{x\sqrt{10}}{4}\)
Gọi H là trung điểm BC \(\Rightarrow SH\perp\left(ABCD\right)\)
Từ H kẻ \(HK\perp AC\Rightarrow\widehat{SKH}=\beta\)
\(SH=\sqrt{SC^2-\left(\frac{BC}{2}\right)^2}=\frac{x\sqrt{6}}{4}\)
\(HK=\frac{1}{2}BO=\frac{1}{4}BD=\frac{x\sqrt{2}}{4}\)
\(\Rightarrow tan\beta=\frac{SH}{HK}=\sqrt{3}\Rightarrow\beta=60^0\)

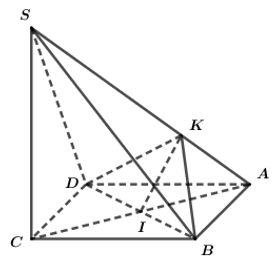
a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt: