Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Ta có: \(\frac{AE}{FE}=\frac{DE}{BE}\)(theo cau a)).
\(\Rightarrow\frac{AE}{FE+AE}=\frac{DE}{BE+DE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{AF}=\frac{DE}{BD}\)(4).
Lại có: \(\frac{KE}{AE}=\frac{DE}{BE}\)(theo câu a)).
\(\Rightarrow\frac{AE}{KE}=\frac{BE}{DE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{KE+AE}=\frac{BE}{DE+BE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{AK}=\frac{BE}{BD}\)(5).
Từ (4) và (5).
\(\Rightarrow\frac{AE}{AF}+\frac{AE}{AK}=\frac{DE}{BD}+\frac{BE}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=\frac{DE+BE}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=\frac{BD}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=1\).
\(\Rightarrow\frac{1}{AF}+\frac{1}{AK}=\frac{1}{AE}\)(điều phải chứng minh).

Để mình quất cho chứ mấy bạn khác tạm thời chưa quất được
a) Do BK // AD, nên \(\dfrac{EK}{AE}=\dfrac{BE}{ED}\left(1\right)\)
Do AB // DG, nên \(\dfrac{AE}{EG}=\dfrac{BE}{ED}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{EK}{AE}=\dfrac{AE}{EG}\Rightarrow AE^2=EK.EG\)
b) Ta có : \(\dfrac{AE}{EK}=\dfrac{DE}{EB}\Rightarrow\dfrac{AE}{AK}=\dfrac{DE}{DB}\left(3\right)\)
Tương tự : \(\dfrac{AE}{AG}=\dfrac{BR}{BD}\left(4\right)\)
Cộng theo từng vế của (3) và (4) ta có:
\(\dfrac{AE}{AK}+\dfrac{AE}{AG}=\dfrac{DE}{DB}+\dfrac{BE}{DB}=\dfrac{BD}{BD}=1\)
c) Đặt AB = a, AD = b thì \(\dfrac{BK}{KG}=\dfrac{a}{CG};\dfrac{CK}{b}=\dfrac{CG}{DG}\)
Nhân theo từng vế của hai đẳng thức trên, ta được :
\(\dfrac{BK}{b}=\dfrac{a}{DG}\) suy ra BK . DG = ab không đổi.
A B C D E K

1. A B C D M N K E F
a) + AN // CD \(\Rightarrow\dfrac{DM}{MN}=\dfrac{MC}{MA}\)
+ AD // CK \(\Rightarrow\dfrac{MK}{MD}=\dfrac{MC}{MA}\)
\(\Rightarrow\dfrac{MD}{MN}=\dfrac{MK}{MD}\) \(\Rightarrow MD^2=MN\cdot MK\)
b) + Qua M kẻ EF // AB // CD
+ AD // CK
=> \(\dfrac{DM}{MK}=\dfrac{AM}{MC}\Rightarrow\dfrac{DM}{DM+MK}=\dfrac{AM}{AM+MC}\) (1)
\(\Rightarrow\dfrac{DM}{DK}=\dfrac{AM}{AC}=\dfrac{AE}{AD}\)
+ ME // AN
\(\Rightarrow\dfrac{DM}{DN}=\dfrac{DE}{DA}\)
=> \(\dfrac{DM}{DN}+\dfrac{DM}{DK}=\dfrac{DE}{DA}+\dfrac{AE}{AD}=1\)
\(\Rightarrow DM\left(\dfrac{1}{DN}+\dfrac{1}{DK}\right)=1\)
\(\Rightarrow\dfrac{1}{DN}+\dfrac{1}{DK}=\dfrac{1}{DM}\)
* Cm : \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
+ \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\) ( theo tính chất dãy tỉ số bằng nhau )
\(\Rightarrow\dfrac{a}{a+b}=\dfrac{c}{c+d}\) ( để giải thích cho (1) )

Giải:
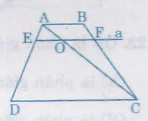
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF
hay AEADAEAD=BFBCBFBC
c) Từ AEEDAEED = BFFCBFFC => AE+EDEDAE+EDED= BF+FCFCBF+FCFC
=> AD