Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

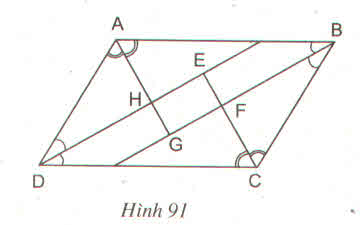
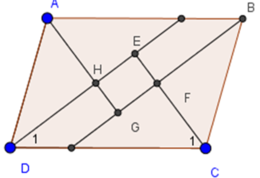
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

Bài giải:
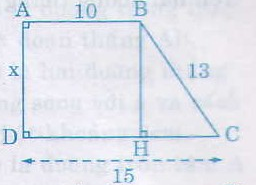
Kẻ BH ⊥ CD
Suy ra DH = 10
Nên HC = 5.
Do đó
BH2 = 132 - 52 = 169 – 25 =144
=> BH = 12
Vậy x = 12.

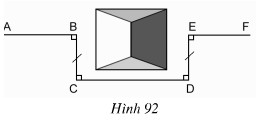
Xét tứ giác BEDC có:
BC // ED (vì cùng ⊥⊥ CD)
BC = ED (gt)
Nên BEDC là hình bình hành.
Hình bình hành BEDC có \(\widehat{C}=90^o\) nên BEDC là hình chữ nhật.
\(\Rightarrow\widehat{CBE}=\widehat{BED}=90^o\)
Khi đó \(\widehat{ABC}+\widehat{CBE}=180^o\) \(\Rightarrow\) A, B, E thẳng hàng.
\(\widehat{BED}+\widehat{DEF}=180^o\Rightarrow\) B, E, F thẳng hàng.
Vậy AB và EF cùng nằm trên một đường thẳng.
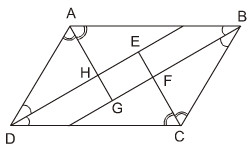


Ta có :
=>
Mà :
=>
=> DM // BF ( ở vị trí đồng vị)
ở vị trí đồng vị)
Hay : EH // FG
cmtt, ta có : GH // EF
=> EFGH là hình bình hành (1).
=>
=> (tổng 3 góc của tam giác AHD)
(tổng 3 góc của tam giác AHD)
=> (đối đỉnh) (2).
(đối đỉnh) (2).
Từ (1) và (2) => EFGH là hình chữ nhật