Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.
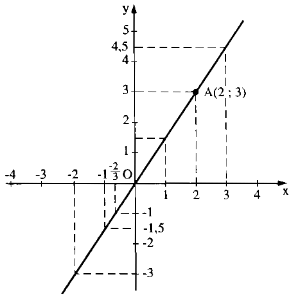
a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) =0
b)\(y=-1\Rightarrow x=\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
\(y=0\Rightarrow x=\dfrac{0}{1,5}=0\)
\(y=4,5\Rightarrow x=\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.

a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) = 0
b)y=−1⇒x=\(\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
b)y=0⇒x==\(\dfrac{0}{1,5}=0\)
y=4,5⇒x=\(\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0

vậy f(1/2)+3.f(2)=1/4 hay 3f(1/2)+9.f(2)=3/4
và f(2)+3.f(1/2)=4
trừ vế theo vế ta đc
8.f(2)=-13/4
suy ra f(2)=-13/32
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!

a)Với x1 = x2 = 1
\( \implies\) \(f\left(1\right)=f\left(1.1\right)\)
\( \implies\) \(f\left(1\right)=f\left(1\right).f\left(1\right)\)
\( \implies\)\(f\left(1\right).f\left(1\right)-f\left(1\right)=0\)
\( \implies\) \(f\left(1\right).\left[f\left(1\right)-1\right]=0\)
\( \implies\) \(\orbr{\begin{cases}f\left(1\right)=0\\f\left(1\right)-1=0\end{cases}}\)
Mà \(f\left(x\right)\) khác \(0\) ( với mọi \(x\) \(\in\) \(R\) ; \(x\) khác \(0\) )
\( \implies\) \(f\left(1\right)\) khác \(0\)
\( \implies\) \(f\left(1\right)-1=0\)
\( \implies\) \(f\left(1\right)=1\)
b)Ta có : \(f\left(\frac{1}{x}\right).f\left(x\right)=f\left(\frac{1}{x}.x\right)\)
\( \implies\) \(f\left(\frac{1}{x}\right).f\left(x\right)=f\left(1\right)=1\)
\( \implies\) \(f\left(\frac{1}{x}\right).f\left(x\right)=1\)
\( \implies\) \(f\left(\frac{1}{x}\right)=\frac{1}{f\left(x\right)}\)
\( \implies\) \(f\left(x^{-1}\right)=\left[f\left(x\right)\right]^{-1}\)

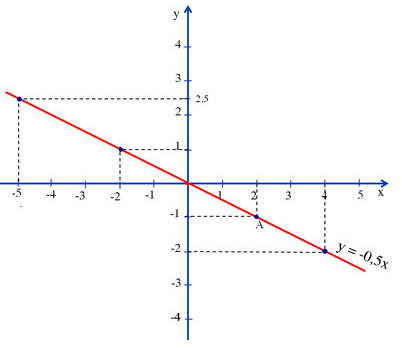
Cho x =2 được y =-2 =>A(2 ;-1) thuộc đồ thị. Vẽ đồ thị
a) Trên đồ thị ta thấy
f(2)=-1
f(-2) =1
f(4)=-2
f(0)=0;
b) Trên đồ thị ta thấy
y=-1 => x=2
y=0 => x=0
y=2,5 => x=-5
c) Khi y dương y > 0 ứng với phần đồ thị nằm trên trục hoành và bên trái trục tung nên x < 0.
Khi y âm : y < 0 ứng với phần đồ thị nằm trên trục hoành và bên phải trục tung nên x > 0

a) f(-2)=5 – 2. (-2) = 5 + 4 = 9;
f(-1) = 5 – 2.(-1) = 5 + 2 = 7;
f(0) = 5 – 2.0 = 5;
f(3) = 5 – 2.3 = 5 – 6 = -1.
b)\(y=5-2x\Rightarrow x=\dfrac{5y}{2}\)
\(y=5\Rightarrow x=\dfrac{5-5}{2}=0\)
\(y=3\Rightarrow x=\dfrac{5-3}{2}=1\)
\(y=-1\Rightarrow x=\dfrac{5-\left(-1\right)}{2}=\dfrac{5+1}{2}=3\)

Ta có: \(\left(0+1\right).f\left(0\right)+3f\left(1-0\right)=2.0+7\)
\(\Rightarrow f\left(0\right)+3f\left(1\right)=7\Rightarrow3f\left(0\right)+9f\left(1\right)=21\) (1)
\(\left(1+1\right)f\left(1\right)+3f\left(1-1\right)=2.1+7\)
\(\Rightarrow2f\left(1\right)+3f\left(0\right)=9\)(2)
Từ (1) và (2) ta được: \(3f\left(0\right)+9f\left(1\right)-2f\left(1\right)-3f\left(0\right)=21-9\)
\(\Rightarrow7f\left(1\right)=12\Rightarrow f\left(1\right)=\frac{12}{7}\)
Khi đó: \(f\left(0\right)=7-3f\left(1\right)=7-3.\frac{12}{7}=\frac{13}{7}\)

Với mọi x khác 0 ta có:
\(\frac{f\left(x\right)}{x}=\frac{f\left(2\right)}{2}=\frac{2}{2}=1\)
=> \(f\left(x\right)=x\)(1)
Với x = 0 thay vào (1) có: f(0) = 0 thỏa mãn
=> f(x) = x thỏa mãn với mọi x

Ta có: \(f\left(4^3+1\right)=4^2-4.3\Rightarrow f\left(65\right)=4\)
Ta có: \(x^3+1=65\)
\(\Rightarrow x^3=64\)\(\Rightarrow x=4\)
Thay \(x=4\)vào hàm số ban đầu ta được
\(f\left(65\right)=4^2-3.4=16-12=4\)
Vậy \(f\left(65\right)=4\)
Ta có: \(f\left(x\right)=x^2-1\)
\(\Rightarrow f\left(1-x_0\right)=\left(1-x_0\right)^2-1\)
\(=x_0^2-2x_0+1-1=x_0^2-2x_0\)
\(=x_0\left(x_0-2\right)\)
\(f\left(1-x_0\right)< 0\Leftrightarrow\)\(x_0\left(x_0-2\right)< 0\)
Mà \(x_0>x_0-2\)nên \(\hept{\begin{cases}x_0>0\\x_0-2< 0\end{cases}}\Leftrightarrow0< x_0< 2\)
Vậy \(0< x_0< 2\)thì \(f\left(1-x_0\right)\)đạt giá trị âm