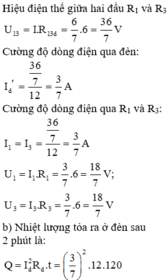Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

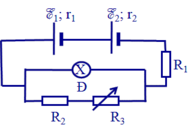
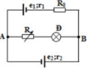
Suất điện động và điện trở trong của bộ nguồn:
E b = E 1 + E 2 = 12 + 6 = 18 ( V ) ; r b = r 1 + r 2 = 0 . 5 + 0 , 25 = 0 , 75 ( Ω )
Điện trở và cường độ định mức của đèn:
R Đ = U Ñ 2 P Ñ = 9 2 9 = 9 Ω ; I đ m = P Ñ U Ñ = 9 9 = 1 A .
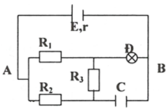
Mạch ngoài có: ( ( R Đ n t R 3 ) / / R 2 ) n t R 1 )
⇒ R N = ( R Ñ + R 3 ) . R 2 R 2 + R 3 + R Ñ + R 1 = ( 9 + 3 ) . R 2 R 2 + 9 + 3 + 2 , 25 = 27 + 14 , 25. R 2 12 + R 2
Đèn sáng bình thường nên: I = I đ m + I ñ m . ( R Ñ + R 3 ) R 2 = E b R N + r b
⇒ 1 + 1. ( 9 + 3 ) R 2 = 18 27 + 14 , 25. R 2 12 + R 2 + 0 , 75 ⇒ R 2 = 12 Ω
Giải bằng chức năng SOLVE.

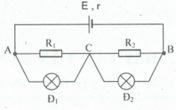
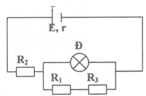
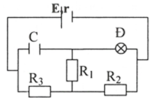
Suất điện động và điện trở trong của bộ nguồn: E b = E 1 + E 2 = 9 + 6 = 15 ( V ) ; r b = r 1 + r 2 = 0 , 5 + 0 , 5 = 1 ( Ω ) . Điện trở và cường độ định mức của đèn: R Đ = U Ñ 2 P Ñ = 6 2 6 = 6 Ω ; I đ m = P Ñ U Ñ = 6 6 = 1 A . Mạch ngoài có: ( ( R 2 n t R 3 ) / / R Đ ) n t R 1 ) ⇒ R N = ( R 2 + R 3 ) . R Ñ R 2 + R 3 + R Ñ + R 1 = ( 4 + R 3 ) .6 4 + R 3 + 6 + 3 , 5 = 59 + 9 , 5 R 3 10 + R 3 Đèn sáng bình thường nên: I = I đ m + U ñ m R 2 + R 3 = E b R N + r b ⇒ 1 + 6 4 + R 3 = 15 59 + 9 , 5 R 3 10 + R 3 + 1 ⇒ R 3 = 2 Ω Giải bằng chức năng SOLVE. |

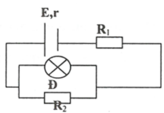
a) Công suất mạch ngoài: \(P=I^2(R_1+R_2)\), mà \(I=\dfrac{E}{R_1+R_2+r}\)
\(\Rightarrow P= (\dfrac{E}{R_1+R_2+r})^2.(R_1+R_2)\), Đặt \(x=R_1+R_2\)
\(\Rightarrow P= (\dfrac{E}{x+r})^2.x=\dfrac{E^2x}{x^2+2xr+r^2}=\dfrac{E^2}{x+\dfrac{r^2}{x}+2r}\)
Pmax khi mẫu số min, mà \(x+\dfrac{r^2}{x}\ge 2\sqrt{x.\dfrac{r^2}{x}}=2r\)(dẫu '=' xảy ra khi \(x=r\))
Vậy \(P_{max}=\dfrac{E^2}{4r}=18W\), khi \(R_1+R_2=R \) \(\Rightarrow R_2=1,5\Omega\)
b. Làm tương tự
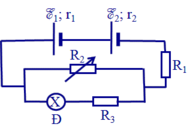
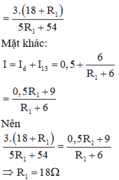
Công suất trên R2: \(P_2=I^2.R_2=(\dfrac{E}{R_1+r+R_2})^2.R_2\)
\(\Rightarrow P_2=\dfrac{E^2.R_2}{(R_1+r)^2+2.(R_1+r)R_2+R_2^2}\)
\(\Rightarrow P_2=\dfrac{E^2}{\dfrac{(R_1+r)^2}{R_2}+R_2+2.(R_1+r)}\)
P2 max khi mẫu số min, mà theo BĐT cô si ta có: \(\dfrac{(R_1+r)^2}{R_2}+R_2 \ge 2(R_1+r)\), dấu '=' xảy ra khi: \(\dfrac{(R_1+r)^2}{R_2}=R_2\)\(\Rightarrow R_2=R_1+r=2,5\Omega\)
\(P_{2max}=\dfrac{E^2}{4(R_1+r)}=14,4W\)