Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tự vẽ hình nhé.
Lấy M, N, P là trung điểm của BE, BD, CE. Chú ý MK, MN là các đường trung bình nên MK || AB, MN || DE. Theo giả thiết \(AB\perp DE\). Suy ra \(MK\perp MN\). Ngoài ra ta có \(MN=\frac12 AB =\frac12 AC=KP\) (Vì K,P là trung điểm EA, EC). Tam giác DEC có hai góc ở đỉnh E,C bằng \(30^\circ\) (vì chúng phụ với hai góc \(60^\circ\)). Thành thử DEC cân ở D. Vậy \(DP\perp DK.\) Tam giác \(DPE\) vuông ở P có góc \(\widehat{DEP}=30^\circ\) nên \(DP=\dfrac12DE\). Mà \(MN=\dfrac12 DE\) (tính chất đường trung bình). Vậy \(MN=DP.\)
Xét hai tam giác vuông \(KMN\) và \(KPD\) có \(KM=KP, MN=PD\) và \(\widehat{KMN}=\widehat{KPD}=90^\circ\). Suy ra \(\Delta KMN=\Delta KPD\) (c.g.c). Từ đó suy ra \(NK=ND\). Ngoài ra \(\widehat{MKN}=\widehat{PKD}.\) Do \(\widehat{MKN}+\widehat{NKC}=\widehat{MKC}=60^\circ\) nên \(\widehat{PKD}+\widehat{NKC}=60^\circ.\) Vậy tam giác \(NKD\) vừa cân vừa có một góc đáy là \(60^\circ\), nên là tam giác đều. Đặc biệt ta có \(NK=ND=NB,\;\widehat{BDK}=60^\circ.\) Suy ra tam giác \(\Delta BDK\) vuông ở \(K\) có góc \(\widehat{BDK}=60^\circ\). Suy ra \(\widehat{KBD}=30^\circ.\) (ĐPCM).

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

1. Phương pháp 1: ( Hình 1)
Nếu thì ba điểm A; B; C thẳng hàng.
2. Phương pháp 2: ( Hình 2)
Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.
(Cơ sở của phương pháp này là: tiên đề Ơ – Clit- tiết 8- hình 7)
3. Phương pháp 3: ( Hình 3)
Nếu AB a ; AC A thì ba điểm A; B; C thẳng hàng.
( Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng
a’ đi qua điểm O và vuông góc với đường thẳng a cho trước
- tiết 3 hình học 7)
Hoặc A; B; C cùng thuộc một đường trung trực của một
đoạn thẳng .(tiết 3- hình 7)
4. Phương pháp 4: ( Hình 4)
Nếu tia OA và tia OB là hai tia phân giác của góc xOy
thì ba điểm O; A; B thẳng hàng.
Cơ sở của phương pháp này là:
Mỗi góc có một và chỉ một tia phân giác .
* Hoặc : Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox ,
thì ba điểm O, A, B thẳng hàng.
5. Nếu K là trung điểm BD, K’ là giao điểm của BD và AC. Nếu K’
Là trung điểm BD thì K’ K thì A, K, C thẳng hàng.
(Cơ sở của phương pháp này là: Mỗi đoạn thẳng chỉ có một trung điểm)
C. Các ví dụ minh họa cho tùng phương pháp:
Phương pháp 1
Ví dụ 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA
(tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm
D sao cho CD = AB.
Chứng minh ba điểm B, M, D thẳng hàng.
Gợi ý: Muốn B, M, D thẳng hàng cần chứng minh
Do nên cần chứng minh
BÀI GIẢI:
AMB và CMD có:
AB = DC (gt).
MA = MC (M là trung điểm AC)
Do đó: AMB = CMD (c.g.c). Suy ra:
Mà (kề bù) nên .
Vậy ba điểm B; M; D thẳng hàng.
Ví dụ 2. Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà AD = AB, trên tia đối
tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED
sao cho CM = EN.
Chứng minh ba điểm M; A; N thẳng hàng.
Gợi ý: Chứng minh từ đó suy ra ba điểm M; A; N thẳng hàng.
BÀI GIẢI (Sơ lược)
ABC = ADE (c.g.c)
ACM = AEN (c.g.c)
Mà (vì ba điểm E; A; C thẳng hàng) nên
Vậy ba điểm M; A; N thẳng hàng (đpcm)
BÀI TẬP THỰC HÀNH CHO PHƯƠNG PHÁP 1
Bài 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối
của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và
CD.
Chứng minh ba điểm M, A, N thẳng hàng.
Bài 2: Cho tam giác ABC vuông ở A có . Vẽ tia Cx BC (tia Cx và điểm A ở
phía ở cùng phía bờ BC), trên tia Cx lấy điểm E sao cho CE = CA. Trên tia đối của tia
BC lấy điểm F sao cho BF = BA.
Chứng minh ba điểm E, A, F thẳng hàng.
Bài 3: Cho tam giác ABC cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia CA lấy điểm
E sao cho CE = BD. Kẻ DH và EK vuông góc với BC (H và K thuộc đường thẳng BC)
Gọi M là trung điểm HK.
Chứng minh ba điểm D, M, E thẳng hàng.
Bài 4: Gọi O là trung điểm của đoạn thẳng AB. Trên hai nửa mặt phẳng đối nhau bờ AB, kẻ
Hai tia Ax và By sao cho .Trên Ax lấy hai điểm C và E(E nằm giữa A và C),
trên By lấy hai điểm D và F ( F nằm giữa B và D) sao cho AC = BD, AE = BF.
Chứng minh ba điểm C, O, D thẳng hàng , ba điểm E, O, F thẳng hàng.
Bài 5.Cho tam giác ABC . Qua A vẽ đường thẳng xy // BC. Từ điểm M trên cạnh BC, vẽ các
đường thẳng song song AB và AC, các đường thẳng này cắt xy theo thứ tự tại D và E.
Chứng minh các đường thẳng AM, BD, CE cùng đi qua một điểm.
PHƯƠNG PHÁP 2
Ví dụ 1: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên
Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung
điểm BD và N là trung điểm EC.
Chứng minh ba điểm E, A, D thẳng hàng.
Hướng dẫn: Xử dụng phương pháp 2
Ta chứng minh AD // BC và AE // BC.
BÀI GIẢI.
BMC và DMA có:
MC = MA (do M là trung điểm AC)
(hai góc đối đỉnh)
MB = MD (do M là trung điểm BD)
Vậy: BMC = DMA (c.g.c)
Suy ra: , hai góc này ở vị trí so le trong nên BC // AD (1)
Chứng minh tương tự : BC // AE (2)
Điểm A ở ngoài BC có một và chỉ một đường thẳng song song BC nên từ (1)
và (2) và theo Tiên đề Ơ-Clit suy ra ba điểm E, A, D thẳng hàng.
Ví dụ 2: Cho hai đoạn thẳng AC và BD cắt nhau tai trung điểm O của mỗi đoạn. Trên tia
AB lấy lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho
D là trung điểm AN.
A B C D E K H F
Nối K với D. Trên tia đối của tia KD lấy điểm F sao cho KD=KF; nối FA và FB.
Gọi giao điểm của đường thẳng vuông góc với AB kẻ từ E là H
Xét \(\Delta\)DEK và \(\Delta\)FAK:
KE=KA
^EKD=^AKF => \(\Delta\)DEK=\(\Delta\)FAK (c.g.c)
KD=KF
=> ^DEK=^FAK (2 góc tương ứng). ^DEK là góc ngoài \(\Delta\)AHE
=> ^DEK=^AHE+^HAE=900+600=1500 => ^FAK=1500
=> ^FAB=^FAK-^BAK=1500-600=900 => ^FAB=900
Lại có: \(\Delta\)DEK=\(\Delta\)FAK (cmt) => DE=FA (2 cạnh tương ứng).
Xét \(\Delta\)AHE: ^AHE=900 => ^HAE+^AEH=900 => ^AEH=900-^HAE=300
Mà ^AEH=^CED (Đối đỉnh) =>^CED=300.
Xét \(\Delta\)DEC: ^DCE=900-^ACB=300 => ^DCE=^CED=300 => \(\Delta\)DEC cân tại D
=> DE=DC. Có DE=FA (cmt) => DC=FA.
Xét \(\Delta\)DCB và \(\Delta\)FAB có:
CB=AB
^DCB=^FAB=900 => \(\Delta\)DCB=\(\Delta\)FAB (c.g.c)
DC=FA
=> DB=FB (2 cạnh tương ứng) => \(\Delta\)DBF cân tại B (1)
=> ^CBD=^ABF (2 góc tương ứng). Ta có: ^CBD+^ABD=^ABC=600
Thay ^CBD=^ABF vào biểu thức trên: => ^ABF+^ABD=^DBF=600 => ^DBF=600 (2)
Từ (1) và (2) => \(\Delta\)DBF là tam giác đều. Mà K là trung điểm DF => BK là trung tuyến
=> BK cũng là đường phân giác của ^DBF => ^KBD=^KBF=^DBF/2=300
=> ^KBD=300.

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
vẽ F sao cho K là trung điểm của DF thì AF//DE,AF=DE.Tam giác DEC có góc E và góc C=30 nên DE=DC,suy ra AF=DC
tam giác BAC=tam giác BCD(c.g.c) nên BF=BD,góc FBA =DBC
Ta lại có góc FBA + góc DBC=DBC+ABD=60 nên góc KBD=30
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
1,

 nên tam giác AGK đều
nên tam giác AGK đều
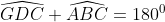
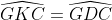 nên GKDC là tứ giác nội tiếp nên
nên GKDC là tứ giác nội tiếp nên 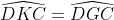
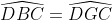 nên
nên 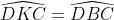

kí hiệu như hình vẽ
vì tam giác AGE vuông tại E có K là trung điểm nên KG=KA
do đó BGKC là hình thang cân
dễ thấy BGDC là tứ giác nội tiếp nên
do đó
mà
do đó KDCB là tứ giác nội tiếp