cho B=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) tìm x nguyên để B nhận giá trị nguyên

\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) tìm x nguyên để B nhận giá trị nguyên

">

K

Khách

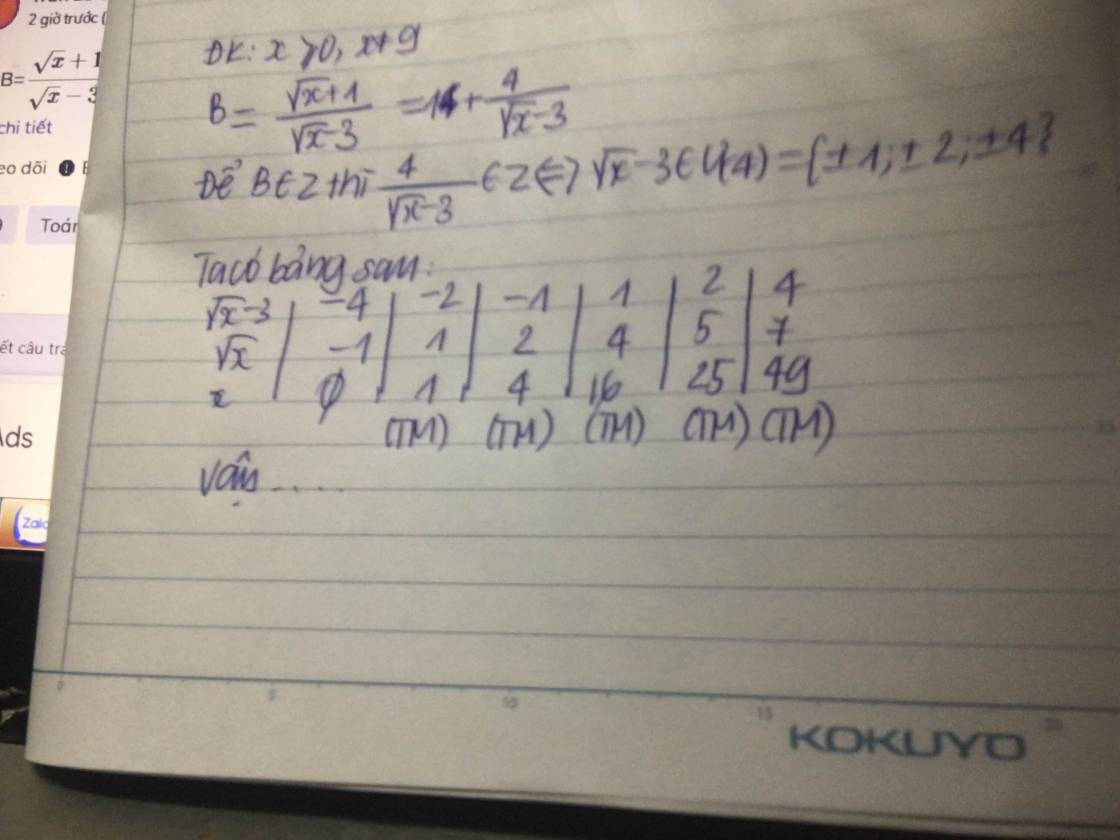
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

TL

Trần Lê Vy

5 tháng 9 2023

cho B=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) tìm x nguyên để B nhận giá trị nguyên

#Hỏi cộng đồng OLM #Toán lớp 9

2

N

nha:)))

5 tháng 9 2023

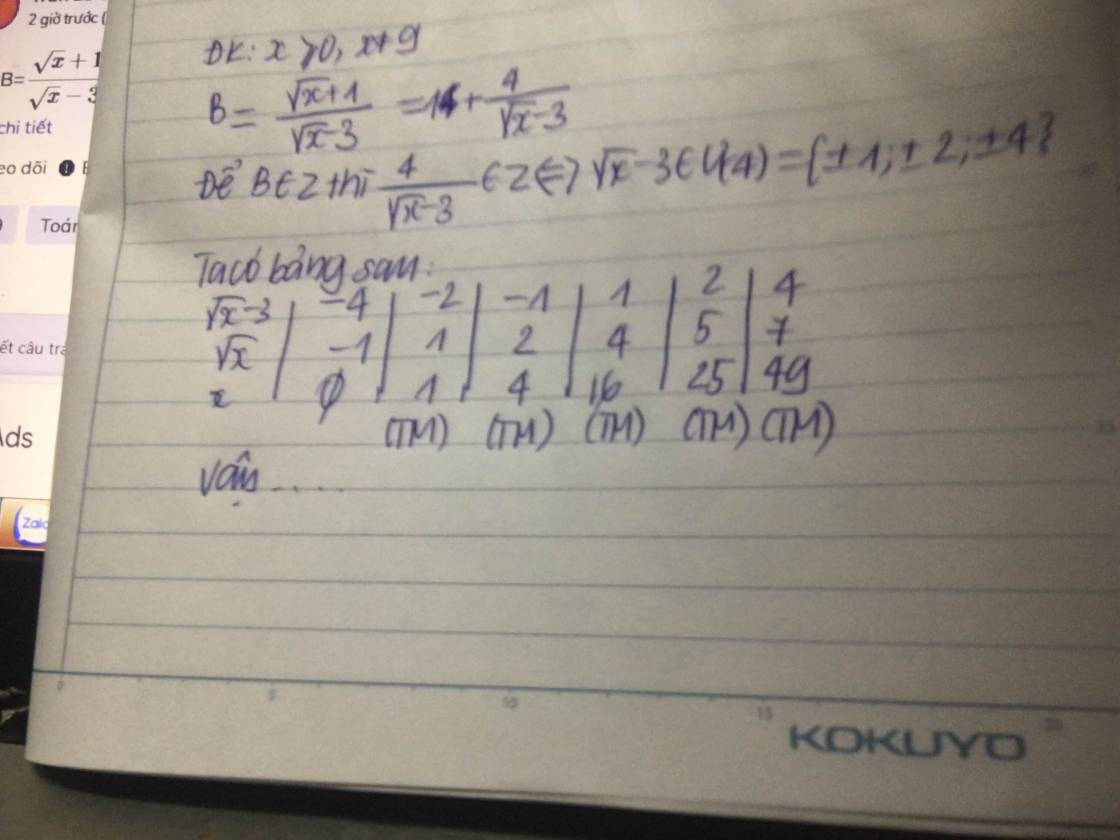
loading...

NL

Nguyễn Lê Phước Thịnh

5 tháng 9 2023

loading...

Các câu hỏi dưới đây có thể giống với câu hỏi trên

TD

Thanh Dii

27 tháng 11 2018 - olm

Cho biểu thức \(Q=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2x-2}{\sqrt{x}-1}\)

a, Rút gọn rồi tìm giá trị nhỏ nhất của Q

b, Tìm các số nguyên x để \(\dfrac{3Q}{\sqrt{x}}\) nhận giá trị nguyên

#Hỏi cộng đồng OLM #Toán lớp 9

1

DP

do phuong nam

27 tháng 11 2018

\(Q=\frac{\sqrt{x}\cdot\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\frac{\sqrt{x}\cdot\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\frac{2\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)

\(Q=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)

\(Q=x+1\)

Không thể tìm được GTLN hay GTNN của Q.

b)

\(\frac{3x+3}{\sqrt{x}}=3\sqrt{x}+\frac{3}{\sqrt{x}}\)

Để \(\frac{3Q}{\sqrt{x}}\) nguyên thì \(\frac{3}{\sqrt{x}}\)nguyên hay \(\sqrt{x}\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)

Vì \(\sqrt{x}\)dương nên \(\sqrt{x}\in\left\{1;3\right\}\)

Vậy x=1, x=9 là các giá trị cần tìm

LT

le thi thuy trang

13 tháng 2 2018 - olm

1.cho biểu thức : F =\(\frac{\sqrt{x}-4}{\sqrt{x}+4}\) tìm x nguyên để F nhận giá trị nguyên

2.cho biểu thức : B= \(\frac{x-9}{x-4}\)tìm x nguyên để B nhận giá trị nguyên

3. cho P = \(\frac{\sqrt{x}-1}{\sqrt{x}+2}\)tìm giá trị nhỏ nhất của P

#Hỏi cộng đồng OLM #Toán lớp 9

0

PH

Phạm Hà Nguyệt Anh

12 tháng 9 2021 - olm

Bài 1: Cho P =\(\frac{7}{\sqrt{x}+3}\) với x \(\ge\)0
a) Tìm x nguyên để P nhận giá trị nguyên
b) Tìm x để P nhận giá trị nguyên

#Hỏi cộng đồng OLM #Toán lớp 9

1

NH

Nguyễn Huy Tú

12 tháng 9 2021

a,\(P=\frac{7}{\sqrt{x}+3}\Rightarrow\sqrt{x}+3\inƯ\left(7\right)=\left\{1;7\right\}\)

\(\sqrt{x}+3\)	1	7
x	loại	16

b, Ta có : \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+3\ge3>0\Rightarrow\hept{\begin{cases}\frac{7}{\sqrt{x}+3}\le\frac{7}{3}\\\frac{7}{\sqrt{x}+3}>0\end{cases}}\)

\(\Rightarrow0< P\le\frac{7}{3}\)mà \(P\in Z\)=> \(P\in\left\{1;2\right\}\)

Với \(P=\frac{7}{\sqrt{x}+3}=1\Rightarrow7=\sqrt{x}+3\Leftrightarrow x=16\)( tm )

Với \(P=\frac{7}{\sqrt{x}+3}=2\Rightarrow7=2\sqrt{x}+6\Leftrightarrow\sqrt{x}=\frac{1}{2}\Leftrightarrow x=\frac{1}{4}\)( ktm )

SG

Sách Giáo Khoa

25 tháng 4 2017

Tìm số \(x\) nguyên để biểu thức \(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) nhận giá trị nguyên ?

#Hỏi cộng đồng OLM #Toán lớp 9

5

TQ

Trần Quang Đài

12 tháng 5 2017

\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)

Để biểu thức đã cho nhận giá trị nguyên buộc \(\dfrac{4}{\sqrt{x}-3}\) nguyên

\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)\in\left\{-4;-2;-1;1;2;4\right\}\)

\(\Rightarrow x\in\left\{1;4;16;25;49\right\}\)

Vậy ......

NT

Nguyen Thuy Hoa

27 tháng 5 2017

Ôn tập Căn bậc hai. Căn bậc ba

Ôn tập Căn bậc hai. Căn bậc ba

BM

Bin Mèo

14 tháng 10 2019 - olm

Bài 2 : Cho A = \(\frac{x\sqrt{x}+1}{x+2\sqrt{x}+1}\) và B = \(\frac{2x+6\sqrt{x}+7}{x\sqrt{x}+1}\)- \(\frac{1}{\sqrt{x}+1}\)( x lớn hơn hoặc bằng 0 )a. Rút gọn A và tính giá trị của A khi x =4b. Rút gọn M =A.B . Tìm M để M > 2 c. Tìm x để M là số nguyên Bài 3 :1) Cho A = \(\frac{2\sqrt{x}+5}{\sqrt{x}-1}\). Tìm x nguyên để biểu thức A nhận giá trị nguyên 2) Cho B = \(\frac{2\sqrt{x}}{x+4}\). Tìm GTLN của B 3) Cho C...

#Hỏi cộng đồng OLM #Toán lớp 9

0

NN

Nguyễn Ngọc Anh

22 tháng 8 2020 - olm

Cho biểu thức:

\(P=\left(1-\frac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\frac{\sqrt{x}+2}{\sqrt{x}+3}+\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{x+\sqrt{x}-6}\right)\)

a)Rút gọn P

b)Tính giá trị P biết \(x=\frac{3\sqrt{5}}{2}\)

c)Tìm giá trị nguyên để P nhận giá trị nguyên

d)Tìm x để P<1

e)Tìm giá trị x để \(P=\sqrt{x}-3\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

PH

Phạm Hà Nguyệt Anh

12 tháng 9 2021 - olm

Bài 1: Cho P = \(\frac{7}{\sqrt{x}+3}\) với x \(\ge\)0
a) Tìm x nguyên để P nhận giá tri nguyên
b) Tìm x để P nhận giá trị nguyên

#Hỏi cộng đồng OLM #Toán lớp 9

0

NT

nguyen thao

25 tháng 7 2020 - olm

Mik đag cần gấp giải giúp vs Cho biểu thức B=\((\frac{\sqrt{x}+1}{\sqrt{x}+2}-\frac{2\sqrt{x}}{\sqrt{x}+2}+\frac{5\sqrt{x}+2}{4-x}):\frac{3\sqrt{x-x}}{x+\sqrt{x}+4}\)a) Rút gọn Bb) Tìm x để B=2c)Tìm x để B nhận giá trị âmCho biểu thức P=\((\frac{x}{x\sqrt{x}-4\sqrt{x}}-\frac{6}{3\sqrt{x}-6}+\frac{1}{\sqrt{x}+2}):(\frac{\sqrt{x}-2+10-x}{\sqrt{x}+2})\)a) Rút gọn Pb)Tìm các giá trị nguyên của x để biểu thức Q=\((-\sqrt{x}-1)\)P nhận đc giá...

#Hỏi cộng đồng OLM #Toán lớp 9

0

PK

Phạm Khánh Huyền

19 tháng 11 2016 - olm

1 tìm các giá trị nguyên của x để N=\(\frac{3}{\sqrt{x}-2}\) nhận giá trị nguyên

2 tìm giá trị của x nguyên để D=\(\frac{\sqrt{x}-2}{\sqrt{x}-3}\) nguyên

#Hỏi cộng đồng OLM #Toán lớp 9

2

AN

alibaba nguyễn

19 tháng 11 2016

Ta có

\(1D=\frac{\sqrt{x}-2}{\sqrt{x}-3}=1+\frac{1}{\sqrt{x}-3}\)

Để cho D nguyên thì \(\sqrt{x}-3\)phải là ước của 1

\(\Rightarrow\sqrt{x}-3=\left(-1;1\right)\)

=> x = (4; 16)

=> D = (0; 2)

AN

alibaba nguyễn

19 tháng 11 2016

1/ Để N nhận giá trị nguyên thì trước hết \(\sqrt{x}-2\)phải là ước của 3

\(\sqrt{x}-2=\left(-3;-1;1;3\right)\)

Thế vào ta tìm được x = (1; 9; 25)

=> N = (- 3; 3;1)

HN

Hồng Nguyễn

28 tháng 7 2018 - olm

Cho biểu thức: P=\(\frac{x\sqrt{x}-8}{x+2\sqrt{x}+4}+3\left(1-\sqrt{x}\right)\), với x\(\ge\)0

a)rút gọn

b)tìm các giá trị nguyên dương của x để biểu thức Q=\(\frac{2P}{1-P}\)nhận giá trị nguyên

#Hỏi cộng đồng OLM #Toán lớp 9

0