Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A H B C
Xét \(\Delta\)ABH và \(\Delta\)CAH có:\(\widehat{AHB}=\widehat{AHC}=90^0;\widehat{BAH}=\widehat{HCA}\)
\(\Rightarrow\Delta ABH~\Delta CAH\left(g.g\right)\Rightarrow\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow AH^2=BH\cdot CH\)
\(\Rightarrowđpcm\)

Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: 
Vậy A H 2 = B H . C H

xét tam giác AHB và tam giác CHA có
góc H = 90 độ
AH là cạnh chung
góc B = góc C (kề bù)
suy ra tam giác AHB đồng dạng tam giác CHA( G.C.G)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH\cdot AH=HB\cdot HC\)
\(\Rightarrow AH^2=HB\cdot HC\)

Xét △ACH vuông tại H và △BAH vuông tại H
Có: \(\widehat{CAH}=\widehat{HBA}\) (cùng phụ với \(\widehat{HAB}\))
=> △ACH ᔕ △BAH (g.g)
\(\Rightarrow\frac{AH}{BH}=\frac{CH}{AH}\)
=> AH . AH = BH . CH
=> AH2 = BH . CH
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh:△HBA=△ABC và góc BAH bằng góc BCA
b)Chứng minh AH2=BH.HC
c)Kẻ phân giác BD của góc ABC(D thuộc AC) cắt AH tại E. Cho AB = 15cm, AC = 20cm. Tính BC,AD, DC,BD
Gọi M là trung điểm ED.Kẻ EF vuông góc AB tại F.Chứng minh 3 đường thẳng EF,BH, AM đòng quy.

Áp dụng các hệ thức lượng trong tam giác vuông ,ta được:
\(AH^2=BH.CH\)
\(AH.BC=AB.AC\)
Lớp 8 chưa học lượng giác mà??
a) Xét tam giác AHC vuông tại H và tam giác AHB vuông tại H
Áp dụng định lý Pytago cho cả 2 tam giác:
Tam giác AHC: AH^2= AC^2 - CH^2 (1)
TAM GIÁC AHB: AH^2 =AB^2 - BH^2 (2)
(1) (2) Suy ra 2AH^2 = AB^2 + AC^2 - CH^2 - BH^2
2AH^2 = BC^2 - CH^2 - BH^2
2AH^2 = (BH+CH)^2 - CH^2 - BH^2
2AH^2 = 2BH.CH
AH^2 = BH.CH
b) Xét tam giác AHB và tam giác CAB:
H^ = A^ = 90 độ
B^ chung
2 tam giác AHB và tam giác CAB đồng dạng trường hợp (g-g)
Suy ra AH/CA = HB/AB= AB/BC
Vậy AH.BC = AB.AC
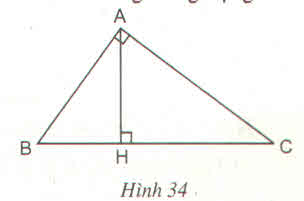


Xét hai tam giác vuông AHB và CHA có:
\(\widehat{ABC}=\widehat{CAH}\) (cùng phụ \(\widehat{ACB}\))
\(\Rightarrow\Delta_vAHB\sim\Delta_vCHA\left(g-g\right)\)
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\Rightarrow AH^2=BH.CH\) (đpcm)