Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét (I) có
ΔAHC nội tiếp đường tròn
AC là đường kính
Do đó: ΔAHC vuông tại H
hay AH\(\perp\)BC
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(AD\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
A B C H D I E
a) Py-ta-go \(\Delta ABH\), ta có : \(AB^2=AH^2+BH^2=25\Rightarrow AB=5\)
\(AH^2=BH.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{16}{3}\)
\(AB.AC=AH.BC\)hay \(5.AC=4.\left(3+\frac{16}{3}\right)\Rightarrow AC=\frac{20}{3}\)
b) HB // DI ( cùng vuông góc AI )
\(\Rightarrow\frac{BH}{DI}=\frac{AB}{AD}=\frac{1}{2}\Rightarrow DI=2BH=6\)
\(\frac{AH}{HI}=\frac{AB}{BD}=1\)kết hợp với AH = 2HE \(\Rightarrow AH=HI=IE=4\)
\(\tan\widehat{IED}=\frac{DI}{IE}=\frac{6}{4}=\frac{3}{2}\)
\(\tan\widehat{HCE}=\frac{HE}{HC}=\frac{8}{\frac{16}{3}}=\frac{3}{2}\)
c) theo câu b, \(\Rightarrow\tan\widehat{IED}=\tan\widehat{HCE}=\frac{3}{2}\)\(\Rightarrow\widehat{IED}=\widehat{HCE}\)
d) \(\widehat{HCE}+\widehat{HEC}=90^o\Rightarrow\widehat{IED}+\widehat{HEC}=90^o\Rightarrow\widehat{DEC}=90^o\Rightarrow DE\perp EC\)
a)
Có: \(AH^2=HB.HC\left(HTL\right)\)
=> \(16=3HC\Rightarrow HC=\frac{16}{3}\)
Lần lượt áp dụng định lí PYTAGO ta được:
\(\hept{\begin{cases}AH^2+HB^2=AB^2\\AH^2+HC^2=AC^2\end{cases}}\)
=> \(\hept{\begin{cases}16+9=AB^2\\16+\frac{256}{9}=AC^2\end{cases}}\)
=> \(\hept{\begin{cases}AB=5\\AC=\frac{20}{3}\end{cases}}\)
b) Có: BH và DI cùng vuông góc với EI
=> BH // DI
=> ÁP DỤNG ĐỊNH LÍ TALET TA ĐƯỢC:
=> \(\frac{AB}{AD}=\frac{AH}{AI}=\frac{BH}{DI}\)
Mà: \(\frac{AB}{AD}=\frac{1}{2}\left(gt\right)\)
=> \(\frac{AH}{AI}=\frac{BH}{DI}=\frac{1}{2}\)
=> \(AH=HI\)
=> \(DI=6;HI=4\)
MÀ: \(EA=AH\left(gt\right)=4\)
=> DIện tích tam giác IED \(=\frac{ID.IE}{2}=\frac{6.12}{2}=36\)
Có: \(HC=\frac{16}{3};HE=8\left(CMT\right)\)
=> Diện tích tam giác HCE \(=\frac{HC.HE}{2}=\frac{16}{3}.8:2=\frac{64}{3}\)
Câu c xem lại đề nha, mình vẽ thì DE ko vuông góc với EC đâu nhaaaaaaa
GIẢI: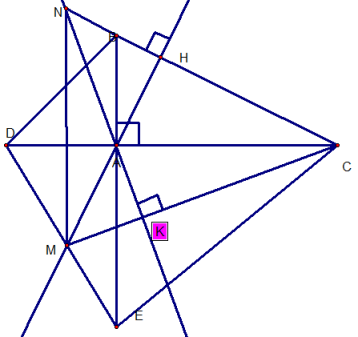
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
A B C H E I D
Ta có \(AB=AD\Rightarrow\Delta ABD\)vuông cân tại A
\(\Rightarrow\widehat{ADI}=45^0\Rightarrow\widehat{EID}=45^0\Rightarrow\Delta IED\)vuông cân tại \(E\Rightarrow IE=ED\)
Xét \(\Delta ABD\)có \(IE\)song song \(AB\Rightarrow\frac{IB}{ID}=\frac{AE}{ED}\)
Mà \(IE=ED\Rightarrow\frac{IB}{ID}=\frac{AE}{IE}\left(đpcm\right)\)
b. Ta có \(AB^2=BH.BC;AC^2=CH.BC\Rightarrow\frac{AB^2}{AC^2}=\frac{BH}{HC}\)
Có \(\widehat{B}+\widehat{C}=90^0;\widehat{BAH}+\widehat{B}=90^0\Rightarrow\widehat{BAH}=\widehat{C}\)
Lại có \(\widehat{BAH}=\widehat{AIE}\)Vì 2 góc ở vị trí so le trong \(\Rightarrow\widehat{C}=\widehat{AIE}\)
Xét \(\Delta ABC\)và \(\Delta EAI\)
có \(\hept{\begin{cases}\widehat{A}=\widehat{E}=90^0\\\widehat{C}=\widehat{AIE}\left(cmt\right)\end{cases}\Rightarrow\Delta ABC~\Delta EAI\left(g-g\right)}\)
\(\Rightarrow\frac{AB}{AC}=\frac{AE}{IE}\)
Lại có \(\frac{AE}{EI}=\frac{IB}{ID}\Rightarrow\frac{IB}{ID}=\frac{AB}{AC}\Rightarrow\frac{IB^2}{ID^2}=\frac{HB}{HC}\left(đpcm\right)\)