Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

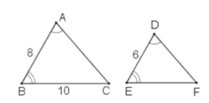
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)

Bài 7:
Đặt a=A'B',b=A'C', c=B'C'
Theo đề,ta có: a/6=b/8=c/10
mà cạnh nhỏ nhất trong tam giác A'B'C' là 9cm
nên b/8=c/10=9/6=3/2
=>b=12cm; c=15cm

A B C D E F 5 7 8 12 45 55
Giải
Vì\(\Delta ABC~\Delta DEF\) nên ta có:
\(\widehat{D}=\widehat{A}=45^o\)
\(\widehat{E}=\widehat{B}=55^o\)
\(\widehat{F}=\widehat{C}=\left(180^o-45^o-55^o\right)=80^o\)
Xét\(\Delta ABC~\Delta DEF\) có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{2}{3}\)
\(\Rightarrow DE=\frac{AB.3}{2}=7,5\)
\(DF=\frac{AC.3}{2}=10,5\)
#hoktot<3#

a: Ta có: ΔA'B'C'∼ΔABC
nên A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/6=B'C'/12=A'C'/8=3/2
=>A'B'=9cm; B'C'=18cm; A'C'=12cm
b: Ta có: ΔA'B'C'∼ΔABC
nên \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{2}\)

ΔABC đồng dạng với ΔDEF
=>AB/DE=BC/EF=AC/DF
=>7/EF=5/DF=3/6=1/2
=>EF=14cm; DF=10cm
ΔABC đồng dạng với ΔDEF
=>AB/DE=BC/EF=AC/DF
=>7/EF=5/DF=3/6=1/2
=>EF=14cm; DF=10cm