Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 5. Gọi số đó là \(\overline{abc}\)
- Xét a = 1,2
b có 9 cách chọn
c có 8 cách chọn
- xét a = 3
+b = 0,1,2
c có 8 cách chọn
+ b = 4
c có 4 cách chọn
=> có : 2 x 8 x 9 + 1 x 3 x 8 + 1 x 1 x4

1. Xét n=1
VT = 12 = 1
VP = \(\dfrac{n.\left(4n^2-1\right)}{3}=\dfrac{1.\left(4.1-1\right)}{3}=1\)
=> VT = VP
=> Mệnh đề đúng.
+) Giả sử với n = k , mệnh đề đúng hay: \(1^2+3^2+5^2+...+\left(2k-1\right)^2=\dfrac{k.\left(4k^2-1\right)}{3}\)+) Ta phải chứng minh với n = k + 1, mệnh đề cũng đúng, tức là: \(1^2+3^2+5^2+...+\left(2k-1\right)^2+\left(2k+1\right)^2=\dfrac{\left(k+1\right).\left(4.\left(k+1\right)^2-1\right)}{3}\\ =\dfrac{\left(k+1\right)\left(4k^2+8k+3\right)}{3}\left(1\right)\)
+) Thật vậy, với n = k + 1, theo giả thiết quy nạp, ta có:
\(1^2+3^2+5^2+...+\left(2k-1\right)^2+\left(2k+1\right)^2=\dfrac{k.\left(4.k^2-1\right)}{3}+\left(2k+1\right)^2\\ =\dfrac{k.\left(4k^2-1\right)+3.\left(2k+1\right)^2}{3}=\dfrac{4k^3-k+12k^2+12k+3}{3}\\ =\dfrac{\left(k+1\right)\left(2k+3\right)\left(2k+1\right)}{3}\\ =\dfrac{\left(k+1\right)\left(4k^2+8k+3\right)}{3}\left(2\right)\)+) Từ (1) và (2) => Điều phải chứng minh
2. +) Xét n = 1
\(< =>4^1+15.1-1=18⋮9\)
=> với n=1 , mệnh đề đúng.
+) Giả sử với n=k , mệnh đề đúng, tức là: \(4^k+15k-1⋮9\)
+) Ta phải chứng minh với n = k + 1 mệnh đề cũng đúng, tức là: \(4^{k+1}+15\left(k+1\right)-1⋮9\)
Thật vậy: với n = k + 1, theo giả thiết quy nạp, ta có:
\(4^{k+1}+15\left(k+1\right)-1=4.4^k+15k+15-1\\ =4.4^k+4.15k-4-3.15k+18=4.\left(4^k+15k-1\right)-\left(45k-18\right)⋮9\)=> Điều phải chứng minh.

1.
Chọn 3 chữ số còn lại từ 7 chữ số còn lại: \(C_7^3=35\) cách
Hoán vị 5 chữ số: \(5!=120\)
Số số thỏa mãn: \(35.120=4200\) số
2.
a.
\(\sqrt{3}sin5x-2sin5x.cos5x=0\)
\(\Leftrightarrow sin5x\left(\sqrt{3}-2cos5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin5x=0\\cos5x=\frac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{5}\\x=\pm\frac{\pi}{30}+\frac{k2\pi}{5}\end{matrix}\right.\)
b.
\(\Leftrightarrow\frac{1}{2}cos2x-\frac{\sqrt{3}}{2}sin2x=cos6x\)
\(\Leftrightarrow cos\left(2x-\frac{\pi}{3}\right)=cos6x\)
\(\Leftrightarrow\left[{}\begin{matrix}6x=2x-\frac{\pi}{3}+k2\pi\\6x=\frac{\pi}{3}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{12}+\frac{k\pi}{2}\\x=\frac{\pi}{24}+\frac{k\pi}{4}\end{matrix}\right.\)

b) TH1: Nếu chọn chữ số 5 làm chữ số hàng đơn vị
Có 8 cách chọn chữ số hàng nghìn
Có 8 cách chọn chữ số hàng trăm
Có 7 cách chọn chữ số hàng chục
-> Có 8.8.7.1=448 số
TH2: Nếu chọn chữ số 0 làm hàng đơn vị
Có 9 cách chọn chữ số hàng nghìn
Có 8 cách chọn chữ số hàng trăm
Có 7 cách chọn chữ số hàng chục
-> Có 9.8.7.1=504 số
=> Có tất cả 448+504=952 số thỏa mãn đề bài

Chọn C
Ta có ![]()
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
![]()
![]()
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà ![]()
![]()
![]()
![]() hoặc
hoặc ![]()
Vì ![]()
![]() nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ

![]()
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
![]()
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
![]()
Vậy xác suất cần tìm là 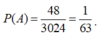

1a) số TM yêu cầu bài toán là: gọi số tự nhiên cần lập có dạng abcd
chọn a có 6 cách
chọn b có 6 cách
chọn c có 6 cách
chọn d có 6 cách
=>6*6*6*6=1296 số Tm
b) số các số tự nhiên lẻ là abc
chọn c là số lẻ có 3 cách
chọn a có 6 cách chọn
chọn b có 6 cách chọn
=>6*6*3=108 cách chọn
câu 2
gọi abcde là số tự nhiên cần lập
chọn a có 6 cách
chọn b có 7 cách
chọn c có 7 cách
chọn d có 7 cách
chọn e có 7 cách
=>6*7*7*7*7=14406 Tm
câu 3
abcdef là số tự nhiên cần lập
chọn a có 7 cách
chọn b có 7 cách
chọn c có 6 cách
chọn d có 5 cách
chọn e có 4 cách
chọn f có 3 cách
=>3*4*5*6*7*7=17640 tm
Ta có: \(A+4=111...15+4=111...19=B\) ( có n chữ số 1)
=> \(A.B+4=A\left(A+4\right)+4=A^2+4A+4=\left(A+2\right)^2\) là số chính phương