Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.

a.Để B là trung điểm AC
\(\Leftrightarrow\left\{{}\begin{matrix}x_b=\frac{x_a+x_c}{2}\\y_b=\frac{y_a+y_c}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{2-3}{2}\\2=\frac{-1+y}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{-1}{2}\\y=5\end{matrix}\right.\)
Gọi AD là trung tuyến tam giác ABC
\(\Rightarrow\)D là trung điểm của BC
\(\Leftrightarrow\left\{{}\begin{matrix}x_d=\frac{x_b+x_c}{2}\\y_d=\frac{y_b+y_c}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_d=\frac{x-3}{2}\\y_d=\frac{2+y}{2}\end{matrix}\right.\)
\(\Leftrightarrow D\left(\frac{x-3}{2};\frac{y+2}{2}\right)\)
Có \(\overrightarrow{AD}\left(\frac{x-7}{2};\frac{y+4}{2}\right)\)
\(\overrightarrow{AO}\left(-2;1\right)\)
Vì O là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{AO}=\frac{2}{3}\overrightarrow{AD}\)
\(\Leftrightarrow\left(-2;1\right)=\left(\frac{x-7}{3};\frac{y+4}{3}\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{x-7}{3}=-2\\\frac{y+4}{3}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

a) Mối liên hệ giữa x và y là: \({x^2} + {y^2} = 5\)
b) Mối liên hệ giữa x và y là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)

Do tọa độ của A là thỏa mãn phương trình của d nên A nằm trên đường thẳng d
Lại có; vectơ B C → ( 3 ; 1 ) là vectơ pháp tuyến của d.
Do đó d là đường thẳng chứa đường cao của tam giác ABC vẽ từ A.
Chọn A.

Hệ: m x + 3 m − 2 y + m − 3 = 0 2 x + m + 1 y − 4 = 0 ⇔ m x + 3 m − 2 y = 3 − m 2 x + m + 1 y = 4
Ta có:
D = m 3 m − 2 2 m + 1 = m 2 − 5 m + 4 = m − 1 m − 4
D x = 3 − m 3 m − 2 4 m + 1
= 3 − m m + 1 − 4 3 m − 2 = − m + 11 = 1 − m m + 11
D y = m 3 − m 2 4 = 4 m − 6 + 2 m = 6 m − 6 = 6 m − 1
Hệ phương trình có nghiệm duy nhất
⇔ D ≠ 0 ⇔ m − 1 m − 4 ≠ 0 ⇔ m ≠ 1 m ≠ 4
⇒ x = D x D = 1 − m m + 11 m − 1 m − 4 = m + 11 4 − m ( 1 ) y = D y D = 6 m − 1 m − 1 m − 4 = 6 m − 4 ( 2 )
Từ 2 ⇒ m − 4 y = 6 ⇔ m y = 6 + 4 y ⇔ m = 6 + 4 y y = 6 y + 4
Thay vào (1) ta được:
x = 6 y + 4 + 11 : 4 − 6 y − 4 = − 6 + 15 y 6 = − 1 − 15 6 y
Đáp án cần chọn là: C

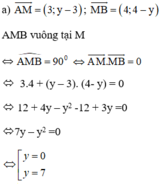
Vậy với M(5; 7) hoặc M(5; 0) thì tam giác ABM vuông tại M.

Vậy P(-5; 2)

a. 5/x-1 có nghĩa <=>
x -1#0 <=> x# 1
b. *f(-2)
Thế x = -2 vô pt
=>y= 5/-3
*f(0)
=>y= 5/-1
*f(2)
=> y= 5
*f(1/3)
=>y= 15
c. *Thế y=-1 vô pt
Ta có: -1= 5/x-1
<=>-(x-1)=5
<=>x=4
*Thế y=1
Ta có:
5/x-1=1
<=>x-1=5
<=> x=6
*Thế y=1/5
Ta có: 5/x-1=1/5
<=>25=x-1
<=>x=26
d. Chỉ cần vẽ trên hệ trục à bạn, không có gì để tính hết

\(\overrightarrow{AB}=\left(1;2\right)\)
\(\overrightarrow{AC}=\left(x;y+5\right)\)
Để A,B,C thẳng hàng thì x/1=y+5/2
=>2x=y+5
=>y=2x-5