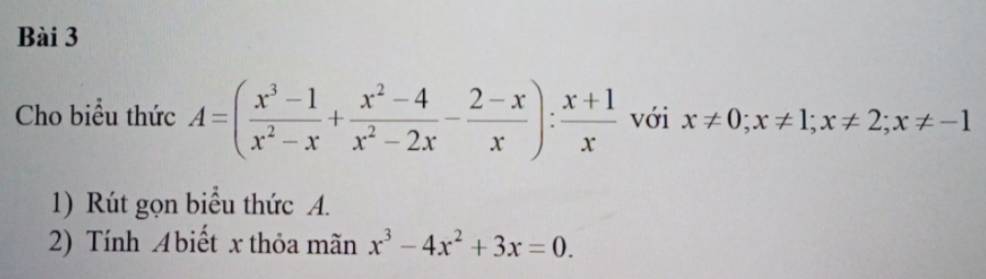Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta dựa trên tính chất của hai đường tròn tiếp xúc trong và tiếp xúc ngoài:
- Hai đường tròn tiếp xúc trong thì điểm tiếp xúc và hai tâm của hai đường tròn thẳng hàng và khoảng cách giữa hai tâm bằng hiệu hai bán kính
- Hai đường tròn tiếp xúc ngoài thì điểm tiếp xúc và hai tâm của hai đường tròn thẳng hàng và khoảng cách giữa hai tâm bằng tổng hai bán kính
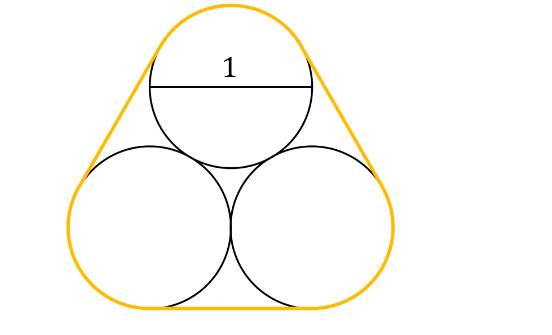
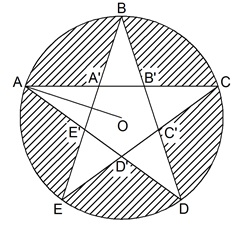
Đặt tên các đỉnh như hình vẽ. Gọi bán kính của sáu đường tròn nhỏ là r, bán kính đường tròn to là R.
Dễ thấy các tâm đường tròn nhỏ A,B,C,D,E,F tạo thành lục giác đều có cạnh là 2r.
Tam giác ABK là tam giác cân vì KA = KB = R - r và có góc K bằng 60o (vì bằng 360o / 6 = 60o). Vậy KAB là tam giác đều.
Suy ra KA = AB.
Hay là R - r = 2r.
=> R = 3 r
=> r = R/3 = 2016/3 = 672 cm
Đáp số: bán kính đường tròn nhỏ bằng 672cm.

a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)



Bài 4:
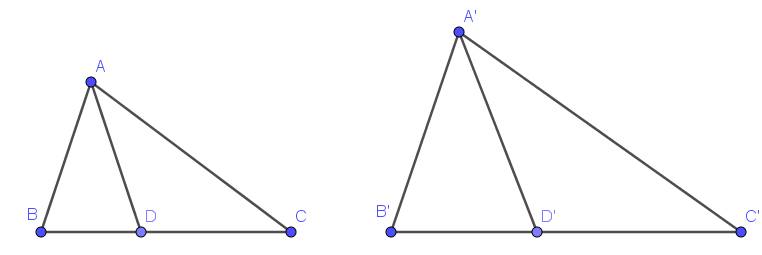
a. Vì $\triangle ABC\sim \triangle A'B'C'$ nên:
$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}(1)$ và $\widehat{ABC}=\widehat{A'B'C'}$
$\frac{DB}{DC}=\frac{D'B'}{D'C}$
$\Rightarrow \frac{BD}{BC}=\frac{D'B'}{B'C'}$
$\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}(2)$
Từ $(1); (2)\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}=\frac{AB}{A'B'}$
Xét tam giác $ABD$ và $A'B'D'$ có:
$\widehat{ABD}=\widehat{ABC}=\widehat{A'B'C'}=\widehat{A'B'D'}$
$\frac{AB}{A'B'}=\frac{BD}{B'D'}$
$\Rightarrow \triangle ABD\sim \triangle A'B'D'$ (c.g.c)
b.
Từ tam giác đồng dạng phần a và (1) suy ra:
$\frac{AD}{A'D'}=\frac{AB}{A'B'}=\frac{BC}{B'C'}$
$\Rightarrow AD.B'C'=BC.A'D'$

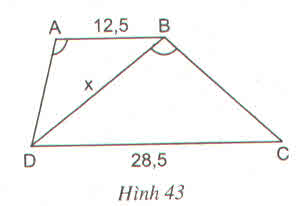
Xét ∆ABD và ∆BDC có:

=> ∆ABD ∽ ∆BDC(trường hợp 3)

=> BD = √(AB.DC) = √(12,5.8,5) = √356,25 => BD = 18,9 cm