
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
1.\(x\left(x+3\right)\)
\(=x^2+3x\)
2.\(3x\left(x+2\right)\)
\(=3x^2+6x\)
3,\(x^2\left(3x-1\right)\)
\(=3x^3-x^2\)
4.\(-5x^3\left(3x^2-7\right)\)
\(=-15x^5+35x^3\)
5.\(3x\left(5x^2-2x-1\right)\)
\(=15x^3-6x^2-3x\)
6.\(-x^2\left(5x^3-x-\dfrac{1}{2}\right)\)
\(=-5x^5+x^3+\dfrac{x^2}{2}\)
7.\(\left(x^2+2x-3\right).\left(-x\right)\)
\(=-x^3-2x^2+3x\)
8.\(4x^3\left(-2x^2+4x^4-3\right)\)
\(=-8x^5+16x^7-12x^3\)
9.\(-5x^2\left(3x^2-2x+1\right)\)
\(=-15x^4+10x^3-5x^2\)
10.\(-4x^5\left(x^3-4x^2+7x-3\right)\)
\(=-4x^8+16x^7-28x^6+12x^5\)
11.\(\left(x+2\right)\left(x+3\right)\)
\(=x^2+3x+2x+6\)
12.\(\left(x-7\right)\left(x-5\right)\)
\(=x^2-5x-7x+35\)
13.\(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
14.\(\left(x-3\right)\left(x^2-2x-1\right)\)
\(x^3-2x^2-x-3x^2+6x+3\)
15.\(\left(2x-1\right)\left(x^2-5x+3\right)\)
\(=2x^3-10x^2+6x-x^2+5x-3\)
16.\(\left(x-5\right)\left(-x^2+x-1\right)\)
\(=-x^3+x^2-x+5x^2-5x+5\)
17,\(\left(\dfrac{1}{2}x+3\right)\left(2x^2-4x-6\right)\)
\(=x^3-2x^2-3x+6x^2-12x-18\)
P/s:mình làm hơi tắt tại bài dài quá:))

`7,`
`a, B+A=4x-2x^2+3`
`-> B=(4x-2x^2+3)-A`
`-> B=(4x-2x^2+3)-(x^2-2x+1)`
`B=4x-2x^2+3-x^2+2x-1`
`B=(-2x^2-x^2)+(4x+2x)+(3-1)`
`B=-3x^2+6x+2`
`b, C-A=-x+7`
`-> C=(-x+7)+A`
`-> C=(-x+7)+(x^2-2x+1)`
`-> C=-x+7+x^2-2x+1`
`C=x^2+(-x-2x)+(7+1)`
`C=x^2-3x+8`
`c,`
`A-D=x^2-2`
`-> D= A- (x^2-2)`
`-> D=(x^2-2x+1)-(x^2-2)`
`D=x^2-2x+1-x^2+2`
`D=(x^2-x^2)-2x+(1+2)`
`D=-2x+3`
`6,`
`a,`
`P+Q=4x-2x^2+3`
`-> Q=(4x-2x^2+3)-P`
`-> Q=(4x-2x^2+3)-(3x^2+x-1)`
`Q=4x-2x^2+3-3x^2-x+1`
`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`
`Q=x^2+3x+4`
`b,`
`x^2-5x+2-P=H`
`-> H= (x^2-5x+2)-(3x^2+x-1)`
`H=x^2-5x+2-3x^2-x+1`
`H=(x^2-3x^2)+(-5x-x)+(2+1)`
`H=-4x^2-6x+3`
`c,`
`P-R=5x^2-3x-4`
`-> R= P- (5x^2-3x-4)`
`-> R=(3x^2+x-1)-(5x^2-3x-4)`
`R=3x^2+x-1-5x^2+3x+4`
`R=(3x^2-5x^2)+(x+3x)+(-1+4)`
`R=-2x^2+4x+3`


Ta có \(\frac{a}{b}-1=\frac{a}{b}-\frac{b}{b}=\frac{a-b}{b}\)
\(\frac{a+2016}{b+2016}-1=\frac{a+2016}{b+2016}-\frac{b+2016}{b+2016}=\frac{a+2016-b-2016}{b+2016}=\frac{a-b}{b+2016}\)
So sánh nứa là ra ok bạn

a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE và AC=BE
b: Xét tứ giác AIEK có
AI//KE
AI=KE
Do đó: AIEK là hình bình hành
Suy ra: Hai đường chéo AE và IK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AE
nên M là trung điểm của IK
hay I.M,K thẳng hàng


\(a)\left(-2.x^2.y\right).\left(5.x.y^4\right)\)
\(=\left(-2.5\right)\left(x^2.x\right)\left(y.y^4\right)\)
\(=-10.x^3.y^5\)
Bậc : \(3+5=8\)
Hệ số : \(-10\)
\(b)\left(\frac{27}{10}.x^4.y^2\right).\left(\frac{5}{9}.x.y\right)^0\)
\(=\frac{27}{10}.x^4.y^2.1\)
\(=\frac{27}{10}.x^4.y^2\)
Bậc : \(4+2=6\)
Hệ số : \(\frac{27}{10}\)
\(c)\left(\frac{1}{3}.x^3.y\right).\left(-xy\right)^2\)
\(=\frac{1}{3}.x^3y.\left(-x\right)^2.y^2\)
\(=\frac{1}{3}.x^3.y.x^2.y^2\)
\(=\frac{1}{3}.\left(x^3.x^2\right).\left(y.y^2\right)\)
\(=\frac{1}{3}x^5.y^3\)
Bậc : \(5+3=8\)
Hệ số : \(\frac{1}{3}\)
Chúc bạn học tốt !!!

Câu 1: (2 điểm) Cho biểu thức:
![]()
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.
Câu 2: (1 điểm)
Tìm tất cả các số tự nhiên có 3 chữ số ![]() sao cho
sao cho ![]()
Câu 3: (2 điểm)
a. Tìm n để n2 + 2006 là một số chính phương
b. Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
Câu 4: (2 điểm)
a. Cho a, b, n thuộc N*. Hãy so sánh ![]()
b. Cho ![]() . So sánh A và B.
. So sánh A và B.
Câu 5: (2 điểm)
Cho 10 số tự nhiên bất kỳ: a1, a2, ....., a10. Chứng minh rằng thế nào cũng có một số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.
Câu 6: (1 điểm)
Cho 2006 đường thẳng trong đó bất kì 2 đường thẳng nào cũng cắt nhau. Không có 3 đường thẳng nào đồng qui. Tính số giao điểm của chúng.
Câu 1: (2 điểm) Cho biểu thức:
![]()
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.
Câu 2: (1 điểm)
Tìm tất cả các số tự nhiên có 3 chữ số ![]() sao cho
sao cho ![]()
Câu 3: (2 điểm)
a. Tìm n để n2 + 2006 là một số chính phương
b. Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
Câu 4: (2 điểm)
a. Cho a, b, n thuộc N*. Hãy so sánh ![]()
b. Cho ![]() . So sánh A và B.
. So sánh A và B.
Câu 5: (2 điểm)
Cho 10 số tự nhiên bất kỳ: a1, a2, ....., a10. Chứng minh rằng thế nào cũng có một số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.
Câu 6: (1 điểm)
Cho 2006 đường thẳng trong đó bất kì 2 đường thẳng nào cũng cắt nhau. Không có 3 đường thẳng nào đồng qui. Tính số giao điểm của chúng.
T.I.C.K nha
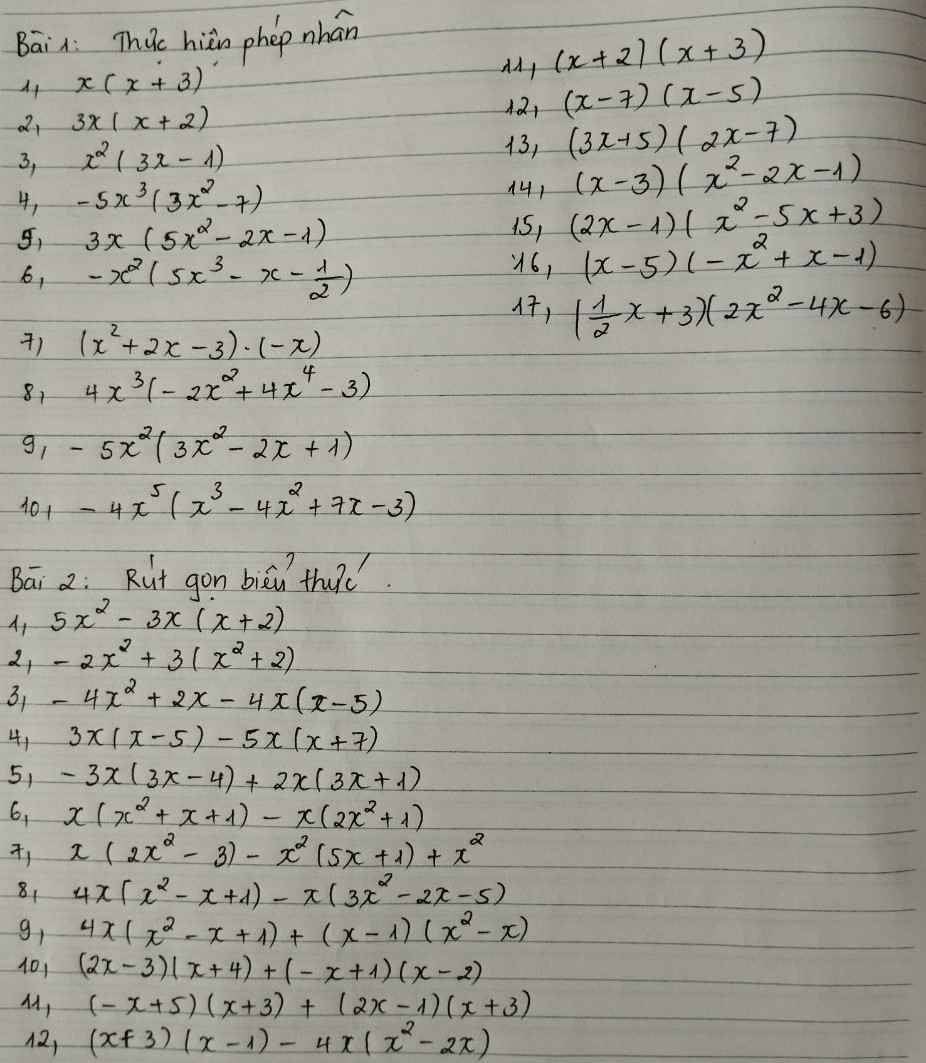




\(\left(\frac{5}{7}-\left|\frac{-7}{5}\right|\right)-\left[\left|\frac{-1}{2}\right|-\left(-\frac{2}{7}+\left|\frac{-1}{10}\right|\right)\right]\)
\(=\left(\frac{5}{7}-\frac{7}{5}\right)-\left[\frac{1}{2}-\left(-\frac{2}{7}+\frac{1}{10}\right)\right]\)
\(=\frac{5}{7}-\frac{7}{5}-\left(\frac{1}{2}+\frac{2}{7}-\frac{1}{10}\right)\)
\(=\frac{5}{7}-\frac{7}{5}-\frac{1}{2}-\frac{2}{7}+\frac{1}{10}\)
\(=\left(\frac{5}{7}-\frac{2}{7}\right)-\left(\frac{7}{5}+\frac{1}{2}-\frac{1}{10}\right)\)
\(=\frac{3}{7}-\frac{9}{5}=\frac{-48}{35}\)