Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C D N I P Q Dễ dàng chứng minh được N,I cùng nằm trên đường trung bình của hình thang (Có thể chứng minh theo tiên đề Ơ-clit)
Khi đó ta có \(NP=IQ=\frac{1}{2}AB=\frac{3}{2}\left(cm\right)\)
NI = PQ - 2NP = 5-3 = 2 (cm)
Chỉ làm r: Câu hỏi của ༺ ๖ۣۜPhạm ✌Tuấn ✌Kiệτ ༻ - Toán lớp 8 | Học trực tuyến
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: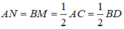 
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: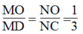 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: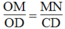 
Hệ quả định lí Ta-lét)
Suy ra: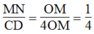 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
Vì đường trung bình của hình thang=5cm nên ta gọi E là trung điểm của BC
Vì ABCD là hình thang
=> AB//CD
Xét tam giác ABC có: E là trung điểm của BC( cách vẽ)
N là trung điểm của AC(gt)
=>NE là đường trung bình của tg ABC
=>NE//BC; \(NE=\frac{1}{2}BC\)
Xét tam giác BDC có: I là trung điểm của BD(gt)
E là trung điểm của BC(cách vẽ)
=>IE là đường trung bình của tg BDC
=>IE//CD;\(IE=\frac{1}{2}BC\)
Vì IE//CD (cmt)
AB//CD(cmt)
=>IE//AB,mà NE//AB(cmt)
=>3 điểm I,N,E thẳng hàng (tiên đề Ơ-clit)
=>IN+NE=IE
=>IN=IE-NE
=>\(IN=\frac{1}{2}CD-\frac{1}{2}AB=\frac{1}{2}\left(CD-AB\right)\)
Gọi K là trung điểm của AD (KE là đường trung bình,E là trung điểm của BC)
=>\(KE=\frac{1}{2}\left(AB+CD\right)=>2KE=AB+CD=>CD=2KE-AB=2.5-3=7\left(cm\right)\)
=>\(IN=\frac{1}{2}\left(CD-AB\right)=\frac{1}{2}\left(7-3\right)=\frac{1}{2}.4=2\left(cm\right)\)