Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác BDC và CEB có
góc E= góc D=90 độ
góc B= Góc C
BC chung
=> tam giác BDC= tam giác CEB(trường hợp cạnh huyền góc nhọn)
=>góc DBC= góc ECB( hai cạnh tương ứng)
mà góc DBC+DBE=góc EBC
góc ECB+ECD=góc BCD
lại có góc EBC=Góc BCD
=>góc DBE=góc BCD
hay góc IBE= cóc ICD
c) có BD và CE cắt nhau tại I
mà trong mộ tam giác ba đường cao đồng quy tại một điểm
=>AI là đường cao hạ từ điingr A của tam giác ABC xuống cạnh BC
=>AI vuông góc với BC

a: Xét ΔBDC vuông tại D và ΔCEB vuông tại E có
BC chung
\(\widehat{DCB}=\widehat{EBC}\)
Do đó: ΔBDC=ΔCEB
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
BD=CE
Do đó:ΔADB=ΔAEC
Suy ra: \(\widehat{IBE}=\widehat{ICD}\)
c: Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại I
Do đó: I là trực tâm của ΔABC
=>AI\(\perp\)BC tại H

vào đây nhé : kiêm tra 45' tiết 46 hình 7 dã chỉnh sửa - Giáo án-Thư viện ...
bạn bấm vào đấy nhé , bài này dài lắm :
nslide.com/giao-an/xem-giao.../kiem-tra-45-tiet-46-hinh-7-da-chinh-sua

Đây chỉ là hướng làm thôi, cần trình bày lại nhé ^^!
1) 2 tam giác này bằng nhau trường hợp cạnh huyền góc nhọn (bạn tự cm nhé)
2) Xét 2 tam giác ABD và ACE (bằng nhau trường hợp cạnh huyền góc nhọn - cạnh huyền là AB và AC, góc nhọn là A^ chung)
=> IBE^ = ICD^
3) Ta có: I là trọng tâm của tam giác ABC => AI là đường cao .Mà AI giao BC = H => AI _|_ BC tại H

a: Xét ΔBDC vuông tại D và ΔCEB vuông tại E có
BC chung
\(\widehat{DCB}=\widehat{EBC}\)
Do đó: ΔBDC=ΔCEB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
DO đó: ΔABD=ΔACE
Suy ra: \(\widehat{IBE}=\widehat{ICD}\)
c: Xét ΔABC có
BD là đường cao
CElà đường cao
BD cắt CE tại I
Do đó: I là trực tâm
=>AI\(\perp\)BC tại H
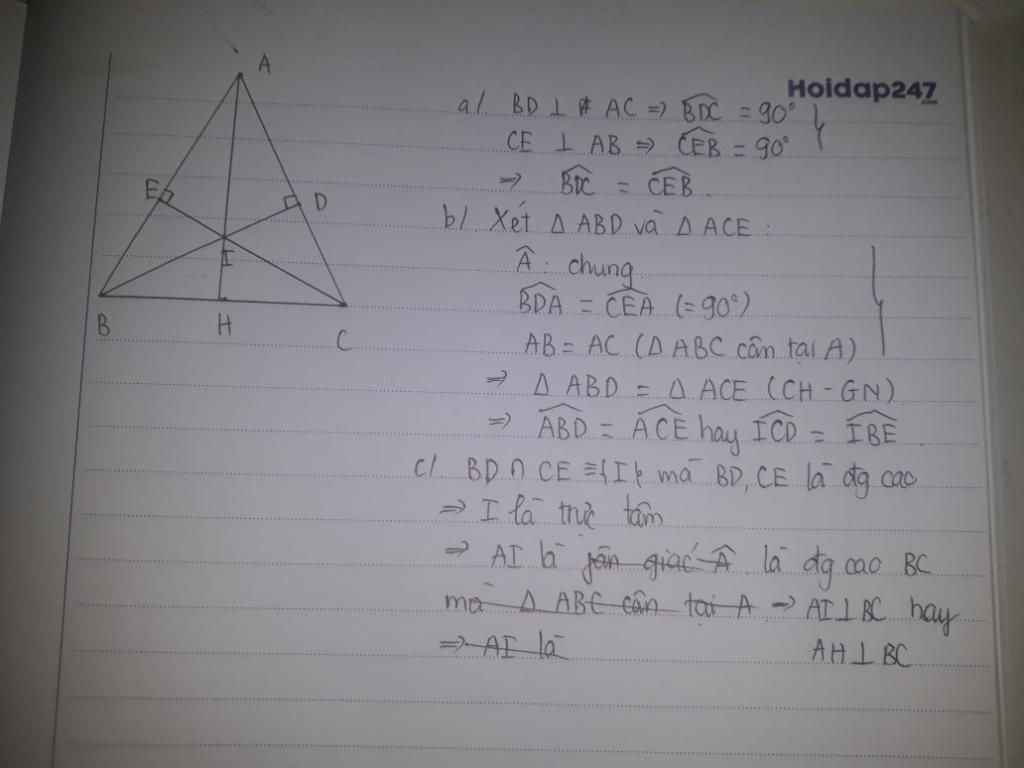
a) Xét 2 tam giác vuông ΔBDC và ΔCEB ta có:
Cạnh huyền BC: chung
\(\widehat{ABC}=\widehat{ACB}\) (△ABC cân tại A)
=> ΔBDC = ΔCEB (c.h - g.n)
b) Có: ΔBDC = ΔCEB (câu a)
=> DC = EB (2 cạnh tương ứng) (1)
Và \(\widehat{ECB}=\widehat{DBC}\) (2 góc tương ứng)
Ta có: \(\widehat{DCI}+\widehat{ECB}=\widehat{ACB}\)
\(\widehat{EBI}+\widehat{DBC}=\widehat{ABC}\)
Mà: \(\widehat{ECB}=\widehat{DBC}\) (cmt)
\(\widehat{ABC}=\widehat{ACB}\) (△ABC cân tại A)
=> \(\widehat{DCI}=\widehat{EBI}\)
Xét ΔEBI và ΔDCI ta có:
\(\widehat{DCI}=\widehat{EBI}\) (cmt)
DC = EB (đã chưng minh ở 1)
\(\widehat{CDI}=\widehat{BEI}\left(=90^0\right)\)
=> ΔEBI = ΔDCI (g - c - g)
=> \(\widehat{IBE}=\widehat{ICD}\) (2 góc tương ứng)
c) Có: ΔEBI = ΔDCI (câu b)
=> BI = CI (2 cạnh tương ứng)
Xét ΔABI và ΔACI ta có:
BI = CI (cmt)
AB = AC (△ABC cân tại A)
AI: cạnh chung
=> ΔABI = ΔACI (c - c - c)
=> \(\widehat{BAI}=\widehat{CAI}\) (2 góc tương ứng)
Hay: \(\widehat{BAH}=\widehat{CAH}\)
Xét ΔABH và ΔACH ta có:
AB = AC (△ABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}\) (cmt)
AH: cạnh chung
=> ΔABH = ΔACH (c - g - c)
=> \(\widehat{AHB}=\widehat{AHC}\) (2 góc tương ứng)
Mà 2 góc này lại là 2 góc kề bù nên
\(\widehat{AHB}=\widehat{AHC}=180^0:2=90^0\)
=> AH ⊥ BC (tại H)
Hay: AI ⊥ BC (tại H)